Анализ рекурсии: как понять и использовать мощь рекурсивных алгоритмов в программировании

---

В современном мире программирования и алгоритмов рекурсия занимает особое место благодаря своей элегантности и мощи. Когда мы впервые сталкиваемся с этим понятием, оно кажется немного загадочным и сложным для понимания. Но как только разбираемся, становится очевидно, что рекурсия — это не только способ решения задач, но и философский подход к их моделированию. В этой статье мы подробно расскажем, что такое рекурсия, как ее анализировать и использовать максимально эффективно, чтобы решать сложные задачи без лишних ошибок и потерь производительности.

Что такое рекурсия и зачем она нужна

Рекурсия, это способность функции вызывать сама себя во время выполнения. В основе лежит идея разбиения сложной задачи на более простую и меньшую по объему аналогичную ей. Такой подход не только упрощает код, но и позволяет добиться высокой читаемости и модульности.

Самое главное — при использовании рекурсии необходимо обеспечить условие завершения вызовов, иначе программа зациклится и приведет к ошибкам, например, "Stack Overflow". Как правило, это базовый случай, который останавливает дальнейшие вызовы и возвращает итоговое значение.

Рассмотрим простую задачу — вычисление факторила числа. Реализовать эту задачу через рекурсию очень просто:

function factorial(n) {
 if (n === 0 || n === 1) {
 return 1; // Базовый случай
 }
 return n * factorial(n ー 1); // Рекурсивный вызов
}

Этот пример показывает слияние классического математического определения и программной реализации.

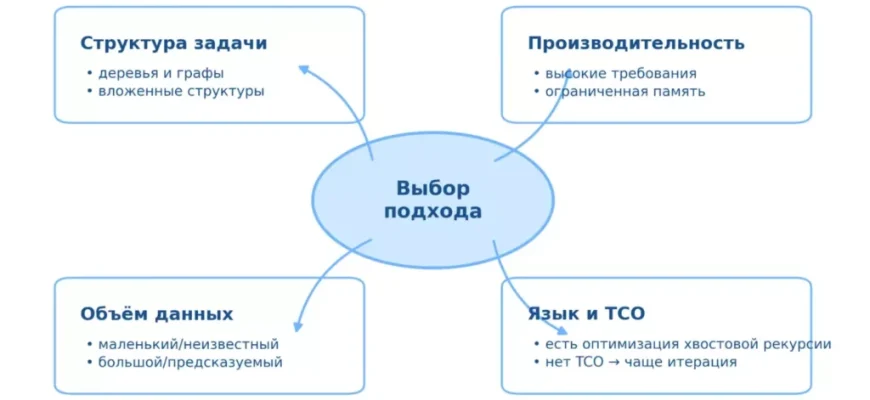
Анализ рекурсии: основные принципы

Чтобы правильно анализировать рекурсивные алгоритмы, необходимо учитывать несколько ключевых аспектов:

• Базовый случай, условие завершения рекурсии, предотвращающее бесконечный вызов.
• Рекурсивный вызов — уменьшение или изменение входных данных, приближающее к базовому случаю.
• План аналитики — определить, как параметры изменяются при каждом вызове, и котировать глубину рекурсии.

Рассмотрим эти моменты подробнее:

Базовый случай

Это условие, при котором рекурсивный вызов прекращается. Обычно оно простое и очевидное, например, при подсчете факториала — ноль или один. Побочным эффектом правильного задания базового случая является предотвращение переполнения стека вызовов.

Изменение параметров

Важно определить, как входные параметры каждой рекурсивной функции изменяются после каждого вызова. Обычно параметры уменьшаются или приближаются к базовому случаю.

Глубина рекурсии

Рассчитаем максимально возможную глубину рекурсии для конкретной задачи. Для этого необходимо объяснить, как параметры изменяются при каждом вызове и сколько их потребуеться для достижения базового случая.

Особенности и риски рекурсивных алгоритмов

Хотя рекурсия очень мощная, она имеет свои особенности и потенциальные риски, о которых важно знать.

Особенность	Описание
Высокое потребление памяти	Каждый вызов функции создает новый стек, что может вызвать переполнение при очень глубокой рекурсии.
Сложность отладки	Рекурсивные алгоритмы труднее отслеживать и тестировать, особенно при сложных условиях.
Может быть медленнее итеративных решений	Из-за накладных расходов на вызовы функций и управление стеком.
Преимущество — лаконичность и ясность кода	Рекурсия позволяет выразить сложные идеи компактно и интуитивно понятно.

Анализ рекурсии на практике: пример разбор задачи

Рассмотрим классический пример, вычисление чисел Фибоначчи. Эта задача показывает, как важно правильно оценивать эффективность рекурсивных вызовов.

Рекурсивная реализация последовательности Фибоначчи

function fibonacci(n) {
 if (n <= 1) {
 return n;
 }
 return fibonacci(n ー 1) + fibonacci(n ー 2);
}

Эта реализация работает правильно, но при больших входных данных становится очень медленной. Проанализируем, почему так происходит:

• Количество вызовов растет по экспоненте, что делает алгоритм неэффективным.
• Глубина рекурсии растет с увеличением n, что может привести к переполнению стека.

Чтобы улучшить данный алгоритм, применяют мемоизацию или итерационный подход.

Оптимизация и анализ эффективности

Улучшенная версия с мемоизацией — пример, как можно грамотно использовать рекурсию:

const memo = {};
function fibonacciMemo(n) {
 if (n in memo) {
 return memo[n];
 }
 if (n <= 1) {
 memo[n] = n;
 return n;
 }
 memo[n] = fibonacciMemo(n ー 1) + fibonacciMemo(n, 2);
 return memo[n];
}

Этот подход существенно сокращает время выполнения, а также снижает глубину рекурсии за счет хранения уже вычисленных значений.

Анализ рекурсии, это важнейший навык программиста, позволяющий разрабатывать эффективные и понятные алгоритмы. Ключевые шаги включают определение базового случая, изменение входных параметров, расчет глубины рекурсии и оценку сложности. Тогда рекурсия станет вашим надежным инструментом для решения самых сложных задач.

Помните, что любая рекурсивная функция должна быть хорошо продумана и протестирована, чтобы избежать нежелательных последствий и максимально эффективно использовать все ее преимущества.

Ответ: Анализ рекурсии помогает понять, как работают алгоритмы, оценить их эффективность, оптимизировать выполнение и избежать возможных ошибок, таких как переполнение стека или чрезмерная сложность. Правильный анализ обеспечивает создание надежных, быстрых и понятных решений, что особенно важно при работе с большими данными и сложными задачами.

Подробнее

рекурсия основы	оптимизация рекурсии	примеры рекурсивных алгоритмов	расчет глубины рекурсии	эффективность рекурсии
использование мемоизации	рекурсия и итерация	учебные задачи по рекурсии	плюсы и минусы рекурсии	стек вызовов