Анализ временной сложности алгоритмов: как понять, насколько они быстры или медленны на разных данных

---

Когда мы говорим о программировании и разработке алгоритмов, одним из ключевых понятий, которое помогает понять эффективность нашей программы, является временная сложность. Это показатель, который описывает, насколько быстро или медленно растет время выполнения алгоритма при увеличении объема входных данных. В этой статье мы подробно расскажем о том, как анализировать временную сложность для различных входных данных, какие факторы на нее влияют и как правильно интерпретировать полученные результаты.

Что такое временная сложность и зачем она нужна?

Понимание временной сложности, это фундаментальный навык для любого разработчика или аналитика. В основном, она помогает оценить, насколько эффективно алгоритм справится с задачей, сталкиваясь с различными объемами данных. Время выполнения алгоритма может значительно варьироваться в зависимости от размера входных данных, их характера и специфики самой задачи.

Например, алгоритм сортировки массива из 10 элементов и из миллиона элементов может отличаться по времени выполнения в сотни или тысячи раз. Поэтому важна не только оценка в общем виде, но и конкретика относительно различных сценариев использования.

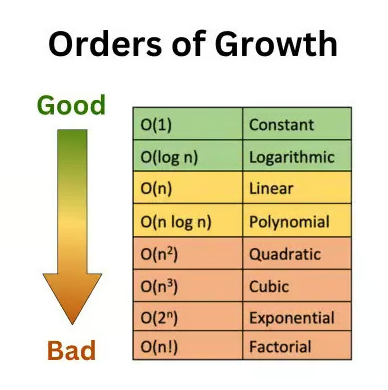
Основные виды временной сложности

• Константная сложность (O(1)): время выполнения не зависит от размера входных данных. Например, доступ к элементу массива по индексу.
• Логарифмическая сложность (O(log n)): время растет медленнее, чем размер данных, например, двоичный поиск.
• Линейная сложность (O(n)): время пропорционально размеру входных данных, как при проходе по массиву.
• Квадратичная сложность (O(n^2)): время растет квадратично, характерна для простых алгоритмов сортировки, таких как пузырьковая сортировка.
• Кубическая сложность и выше: встречаются крайне редко и только в очень сложных алгоритмах.

Как анализировать влияние различных входных данных?

Очень важно понять, что одна и та же реализация алгоритма может вести себя по-разному в зависимости от типа входных данных. Временная сложность — это не только характеристика алгоритма, но и его поведения на конкретных данных. Разделим входные данные на несколько категорий:

• Лучший случай: самый быстрый сценарий работы алгоритма.
• Средний случай: ожидаемое поведение при случайных данных;
• Худший случай: наихудшая ситуация, которая заставляет алгоритм работать максимально долго.

Рассмотрим подробнее, что влияет на каждую категорию и как это влияет на анализ.

Влияние различных данных на временную сложность

Лучший случай

Например, при поиске элемента в отсортированном массиве с помощью двоичного поиска, лучший случай — это когда искомый элемент находится в середине, и алгоритм завершает поиск за одну итерацию. В этом случае сложность может быть O(1), хотя в общем случае она O(log n).

Средний случай

Для большинства алгоритмов и типовых сценариев, средний случай определяется как среднее по вероятностям всех возможных вариантов входных данных. Например, при сортировке массива, где порядок элементов случайный, считается, что алгоритм работает примерно за O(n log n).

Худший случай

Худшая ситуация — это сценарий, при котором алгоритм работает максимально долго. Например, сортировка пузырьком в отсортированном в обратном порядке массиве занимает O(n^2). Анализ худшего случая важен для гарантии надежной работы системы даже при неблагоприятных данных.

Как изучить и провести анализ временной сложности?

Процесс анализа включает несколько шагов:

1. Определить основные операции: что влияет на время выполнения? Обычно это сравнения, присвоения, обмены элементов.
2. Проанализировать поведение при различных размерах данных: построить зависимость времени от размера входных данных.
3. Использовать математические оценки: выразить рост времени через асимптотическую нотацию (O-нотация).
4. Провести экспериментальные испытания: реализовать алгоритм и замерить время на тестовых данных.

Тип входных данных	Оценка сложности	Описание
Отсортированный массив	O(1) ─ лучший случай для поиска, O(n log n) — сортировка	Массив уже отсортирован, что влияет на скорость поиска и сортировки
Массив в случайном порядке	O(n log n) для большинства сортировок	Средний сценарий, типичный для большинства практических случаев
Массив в обратном порядке	O(n^2) для пузырька, O(n log n) для быстрой сортировки	Худший случай для простых алгоритмов сортировки, при этом некоторые методы остаются эффективными
Массив с повторяющимися элементами	Зависит от алгоритма, в среднем O(n log n)	Многие алгоритмы работают быстрее или медленнее в зависимости от повторяющихся данных

Практические советы по анализу и оптимизации

Чтобы не просто теоретически оценивать сложность алгоритма, важно применять практические методы:

• Профилирование кода: использование инструментов для замера времени выполнения.
• Тестирование на масштабируемых данных: запуск алгоритма на данных разного размера и анализ результатов.
• Использование аналитических формул: для сложных алгоритмов, аналитический расчет, помогающий предсказать поведение.
• Оптимизация кода: например, выбор более эффективных структур данных или подходов.

Анализ временной сложности, это не только формальные вычисления, но и практический навык, необходимый для проектирования эффективных решений. Важно учитывать, что разные входные данные могут значительно влиять на поведение алгоритма. Постоянное тестирование, сравнение и понимание особенностей данных помогают выбрать оптимальный алгоритм или внести изменения для повышения эффективности.

Подробнее

Оптимизация алгоритмов по сложности	Сравнение алгоритмов сортировки	Как измерить время выполнения кода	Профилирование программ	Влияние данных на сложность алгоритмов
Лучший, средний и худший случай	Аналитика временной сложности	Тестирование производительности	Асимптотический анализ	Обработка больших данных
Профиль выполнения алгоритмов	Опасности неправильной оценки	Методы ускорения алгоритмов	Практическая оптимизация кода	Реальные сценарии тестирования