Bucket Sort: Эффективное распределение для сортировки массивов

В этой статье мы погрузимся в мир алгоритмов сортировки, фокусируясь на методе Bucket Sort. Учитывая, что существует множество способов упорядочить данные, именно Bucket Sort обладает своими уникальными особенностями, которые делают его особенно привлекательным для определенных задач. Мы расскажем о том, как этот алгоритм работает, его преимуществах и недостатках, а также о примерах применения.

Что такое Bucket Sort?

Bucket Sort, или «сортировка ведрами», — это алгоритм, который использует принцип распределения для сортировки элементов массива. Идея заключается в том, чтобы разбить множество чисел на несколько подмножество (или ведер), а затем отсортировать каждое из них индивидуально. В процессе сортировки ведер мы можем применять другие методы, такие как сортировка вставками или быстрая сортировка, для получения окончательного результата.

Принцип работы Bucket Sort

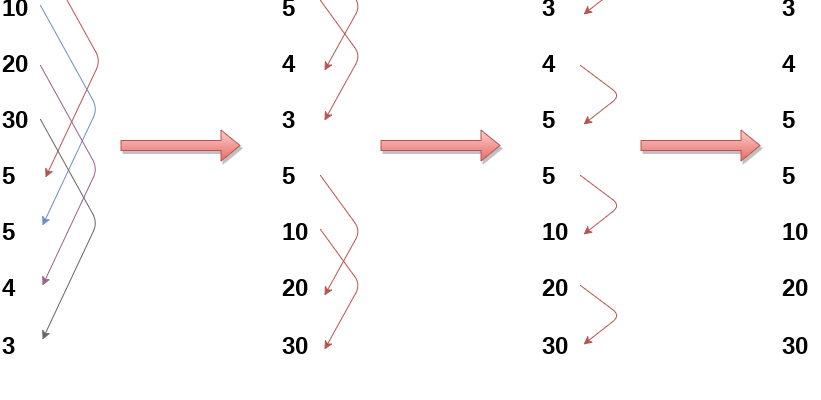
В Bucket Sort мы сначала определяем диапазон значений элементов и создаем «ведра» для этих значений. Затем мы распределяем элементы в ведра в зависимости от их значений. После распределения мы сортируем каждое ведро отдельно и, в конце концов, объединяем их в один отсортированный массив. Этот подход особенно эффективен, когда распределение элементов относительно равномерно.

1. Определение максимального и минимального значения в массиве.
2. Создание ведер в зависимости от диапазона значений.
3. Распределение элементов по ведрам.
4. Сортировка отдельных ведер.
5. Объединение отсортированных ведер в финальный массив.

Почему выбрать Bucket Sort?

Одним из главных преимуществ Bucket Sort является его эффективность при определенных условиях. Если массив изначально достаточно равномерно распределен, производительность алгоритма значительно улучшается. Также стоит отметить, что Bucket Sort может быть адаптирован для работы на параллельных обработках, что делает его актуальным для работы с большими объемами данных.

Сложность алгоритма

Сложность Bucket Sort можно оценить следующим образом:

Сложность	Лучший случай	Средний случай	Худший случай
Время	O(n + k)	O(n + k)	O(n²)
Память	O(n + k)	O(n + k)	O(n + k)

Где n — количество элементов в массиве, а k — количество ведер. Как видно, в идеальных условиях время выполнения может быть значительно ниже по сравнению с классическими алгоритмами сортировки.

Недостатки Bucket Sort

Несмотря на свои преимущества, Bucket Sort имеет и недостатки. Одна из основных проблем заключается в том, что алгоритм требует предварительных знаний о диапазоне значений в массиве, что может не всегда быть доступно. Кроме того, в случае неравномерного распределения значений, производительность может значительно ухудшаться, так как некоторые ведра могут содержать гораздо больше элементов, чем другие.

Пример реализации Bucket Sort

Теперь давайте рассмотрим пример реализации алгоритма на языке Python:

def bucket_sort(arr):
 max_value = max(arr)
 min_value = min(arr)
 bucket_range = (max_value ⎯ min_value) // len(arr) + 1
 buckets = [[] for _ in range(len(arr))]

 for num in arr:
 index = (num ⎯ min_value) // bucket_range
 buckets[index].append(num)

 sorted_array = []
 for bucket in buckets:
 sorted_array.extend(sorted(bucket))
 
 return sorted_array

Пример использования
array = [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.55, 0;25, 0.68]
sorted_array = bucket_sort(array)
print(sorted_array)

В этом примере мы создаем ведра в зависимости от диапазона значений, затем распределяем входящие данные и сортируем их с помощью встроенной функции sorted. Финальный результат объединяется в отсортированный массив.

Где применяется Bucket Sort?

Bucket Sort находит применение в различных областях, таких как:

• Сортировка больших объемов числовых данных.
• Обработка распределенных данных в реальном времени.
• Сортировка графиков и изображений на основе пикселей.
• Финансовые приложения для обработки больших наборов данных, например, цен акций.

Сравнение Bucket Sort с другими алгоритмами

В процессе обсуждения сортировочных алгоритмов, нам не обойтись без сравнений. Сравним Bucket Sort с более известными алгоритмами, такими как Quick Sort и Merge Sort:

Алгоритм	Лучший случай	Средний случай	Худший случай	Дополнительная память
Bucket Sort	O(n + k)	O(n + k)	O(n²)	O(n + k)
Quick Sort	O(n log n)	O(n log n)	O(n²)	O(log n)
Merge Sort	O(n log n)	O(n log n)	O(n log n)	O(n)

Как видно из таблицы, каждый алгоритм имеет свои особенности и сильные стороны, и выбор конкретного алгоритма зависит от задачи, требуемой производительности и объема данных.

Bucket Sort — это мощный инструмент для сортировки, который, при правильном использовании, может значительно улучшить производительность обработки больших данных. Однако это не универсальное решение, и нам важно проводить тщательный анализ перед выбором алгоритма для конкретной задачи. Если вы столкнулись с задачей сортировки, не забывайте о Bucket Sort и его уникальных возможностях.

Подробнее

Быстрая сортировка	Сортировка слиянием	Сортировка пузырьком	Алгоритм диаграмм	Сортировка кучей
Оптимизация алгоритмов	Структуры данных	Программирование на Python	Алгоритмика	Обработка данных