- Bucket Sort: Как эффективно сортировать данные с помощью распределения
- Что такое Bucket Sort и зачем он нужен?
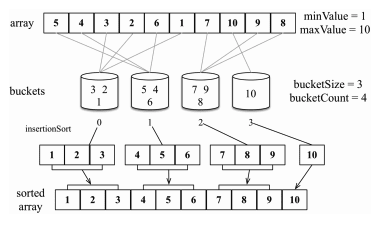
- Основная идея и принцип работы
- Когда использовать Bucket Sort?
- Пошаговый пример работы алгоритма
- Описание ситуации
- Этап первый: создание ведер
- Этап второй: распределение элементов
- Этап третий: локальная сортировка ведер
- Этап четвертый: объединение
- Преимущества и недостатки Bucket Sort
- Практические советы по использованию Bucket Sort
Bucket Sort: Как эффективно сортировать данные с помощью распределения
Когда речь заходит о сортировке данных, стандартные алгоритмы вроде быстрой сортировки или сортировки слиянием — это лишь вершина айсберга. Но в мире алгоритмов есть особенные методы, которые используют идеи распределения элементов по "корзинам" или "ведрам" — один из них заслуженно считается одним из наиболее эффективных при определённых условиях.
Представьте ситуацию: у нас есть огромное количество чисел, и нужно быстро упорядочить их по возрастанию. Стандартные методы могут работать, но их эффективность может стать проблемой при больших объёмах данных или специальных требованиях к скорости. Здесь на сцену выходит Bucket Sort — алгоритм, который основан на распределении элементов по "корзинам", после чего каждый "ведро" сортируется отдельно, а затем конкатенируется в итоговую последовательность. Такой подход позволяет значительно ускорить процесс сортировки, особенно при равномерном распределении входных данных.
Что такое Bucket Sort и зачем он нужен?
Bucket Sort, или сортировка по ведрам, — это алгоритм сортировки, реализуемый на основе идеи разделения набора элементов на несколько «ведер» (корзин), внутри которых применяются более простые алгоритмы сортировки. В результате уменьшается общее время выполнения, так как каждый кусок данных обрабатывается отдельно и быстро.
Данный алгоритм особенно эффективен, когда входные данные имеют равномерное распределение, или когда необходимо обработать большие объёмы данных, разделяемых по диапазонам.
Как работает Bucket Sort? — алгоритм разделяет входные элементы по диапазонам, помещая их в соответствующие "корзины", после чего каждое ведро сортируется, и всё объединяется в итоговый массив.
Основная идея и принцип работы
Основная идея алгоритма, это распределение элементов по ведрам, которые соответствуют определённым диапазонам значений. Например, при сортировке чисел от 0 до 1 можно создать 10 ведер, каждый из которых вобьёт числа в диапазон 0.0–0.1, 0.1–0.2 и т.д.. После этого каждое ведро сортируется отдельно, и результат объединяеться в один массив.
Ключевые этапы работы:
- Разделение диапазона значений: определение, какие области охватывают ведра;
- Распределение элементов: помещение каждого элемента в соответствующее ведро;
- Локальная сортировка: сортировка каждого ведра, чаще всего — простым алгоритмом, например, вставками;
- Объединение результатов: последовательное соединение отсортированных ведер в итоговую последовательность.
Когда использовать Bucket Sort?
Этот алгоритм наиболее эффективен в следующих случаях:
- Равномерное распределение данных: когда значения расположены равномерно между минимальным и максимальным значением.
- Большие объемы данных: когда нужно быстро отсортировать массив из тысяч или миллионов элементов.
- Числовые значения в диапазоне: например, числа с плавающей точкой или целые числа в диапазоне.
- Готовность к многоступенчатой сортировке: особенно эффективен при необходимости использования уже закрепленных методов внутри ведер.
Если же данные распределены неравномерно, или диапазон очень большой, эффективность Bucket Sort может снизиться, и предпочтение стоит отдать другим алгоритмам.
Пошаговый пример работы алгоритма
Описание ситуации
Рассмотрим пример сортировки чисел с плавающей точкой, лежащих в диапазоне от 0 до 1. Пусть у нас есть следующий массив:
| Массив |
|---|
| 0.42, 0.32, 0.23, 0.52, 0.25, 0.47, 0.55, 0;31, 0.43, 0.37 |
Этап первый: создание ведер
Д значений создаем 5 ведер, охватывающих диапазоны:
- 0.0–0.2
- 0.2–0.4
- 0.4–0.6
- 0.6–0.8
- 0.8–1.0
Этап второй: распределение элементов
Помещаем каждый элемент в соответствующее ведро:
| Ведро | Элементы |
|---|---|
| 0.0–0.2 | 0.23, 0;25 |
| 0.2–0.4 | 0;32, 0.31, 0.37, 0.23 |
| 0.4–0.6 | 0.42, 0.47, 0.52, 0.43, 0.55 |
| 0.6–0.8 | |
| 0.8–1.0 |
Этап третий: локальная сортировка ведер
Для каждого ведра применим сортировку вставками, чтобы упорядочить списки внутри ведер:
- 0.23, 0.25
- 0.31, 0.32, 0.37, 0.23 → отсортируем по возрастанию: 0.23, 0.31, 0.32, 0.37
- 0.42, 0.43, 0.47, 0.52, 0.55
Этап четвертый: объединение
Объединяем все отсортированные ведра в итоговый массив:
| 0.23, 0.25, 0.23, 0.31, 0.32, 0.37, 0.42, 0.43, 0.47, 0.52, 0;55 |
Обратите внимание, что есть повторяющиеся элементы — их можно оставить, или убрать в зависимости от требований.
Преимущества и недостатки Bucket Sort
Преимущества:
- Высокая скорость при равномерном распределении данных.
- Параллельная обработка ведер — высокая эффективность на многопроцессорных системах.
- Гибкость в использовании с разными типами данных, особенно числовыми.
Недостатки:
- Эффективность падает при нерегулярном распределении элементов.
- Не подходит для больших диапазонов без правильного масштабирования.
- Неустойчивость к неправильному определению количества ведер.
Практические советы по использованию Bucket Sort
Если вы решились использовать Bucket Sort в своих проектах, стоит учитывать несколько важных аспектов для достижения максимальной эффективности:
- Определяйте диапазон и количество ведер: чем больше ведер — тем выше точность, но и больше затрат.
- Используйте подходящий локальный алгоритм сортировки: вставками или сортировкой пузырьком для маленьких ведер.
- Оценивайте распределение данных заранее: его равномерность существенно влияет на итоговую скорость.
Bucket Sort — это мощный инструмент в арсенале разработчика, который позволяет значительно ускорить сортировку при правильных условиях. Его эффективность особенно проявляется при равномерно распределённых числах, больших объемах данных и необходимости многопроцессорной обработки. Однако важно правильно подобрать параметры и учитывать особенности конкретных данных. В итоге, этот алгоритм может стать вашим союзником при решении задач, где скорость — приоритет, а данные подходят под его специфику.
Подробнее
| Эффективность Bucket Sort | Плюсы и минусы алгоритма | Примеры использования | Часто задаваемые вопросы | Лучшие практики |
| Оптимальные сценарии | Сравнение с другими сортировками | Применение для чисел с плавающей точкой | Ошибки при реализации | Советы по настройке ведер |
| Варианты локальных алгоритмов | Обработка больших диапазонов | Параллельная обработка ведер | Нюансы при нерегулярном распределении | Шаги по повышению эффективности |
| История создания | Современные модификации | Практические кейсы | Интеграция в системы | Инструменты для автоматической настройки |
| Обзор лучших реализаций | Поддерживаемые языки программирования | Обзор популярных библиотек | Стоимость и эффективность | Реальные отзывы и кейсы |