Исследование рекурсии: как понять и применить один из самых загадочных принципов программирования

---

Когда мы сталкиваемся с понятием «рекурсия» в программировании‚ оно зачастую вызывает у новичков легкое замешательство и даже некоторый страх. Зачем писать функцию‚ которая вызывает сама себя? Почему это считается мощным инструментом‚ и как правильно его использовать? В этой статье мы вместе раскроем все тайны рекурсии‚ разберем ее особенности‚ преимущества и сложности‚ а также приведем практические примеры‚ которые помогут вам освоить этот важный концепт.

Рекурсия, это не просто функция‚ вызывающая саму себя. Это уникальный принцип‚ который позволяет решать сложные задачи‚ разбивая их на более простые подзадачи‚ копирующие изначальную проблему. Представьте себе зеркала‚ смотрящие друг в друга — так и рекурсивный вызов работает‚ создавая бесконечную‚ но управляемую цепочку‚ которая решает общий вопрос по частям.

Что такое рекурсия? Теоретические основы

---

Объясняя простыми словами‚ рекурсия — это метод в программировании‚ с помощью которого функция решает задачу‚ вызывая сама себя с более простыми или меньшими по размеру входными данными. Важно‚ чтобы каждый вызов приближал нас к условию завершения — так называемой базе рекурсии. Это условие‚ при котором дальнейшие вызовы не нужны‚ и решение принимает конечный вид.

Можно представить это как цепочку‚ в которой каждый звено зависит от предыдущего‚ и завершение цепи — это базовое условие. В противном случае‚ без правильного базового условия‚ рекурсия могла бы стать бесконечной и привести к ошибке переполнения стека.

Основные компоненты рекурсивной функции

Компонент	Описание
Базовое условие	Условие‚ при котором рекурсия прекращается. Обеспечивает завершение рекурсивных вызовов.
Рекурсивный вызов	Механизм вызова функции самой себя с измененными параметрами для решения меньшей подзадачи.
Параметры	Входные данные функции‚ меняющиеся при каждом вызове‚ стремящиеся к базовому условию.

Практическая часть: зачем применять рекурсию?

---

Рекурсия отлично подходит для решения задач‚ которые имеют естественную рекурсивную природу или требуют обхода структур данных‚ таких как деревья или графы. Она позволяет писать лаконичный и понятный код‚ когда итеративные решения становятся слишком громоздкими и сложными.

Рассмотрим несколько ситуаций‚ в которых рекурсия становиться незаменимой:

• Обход деревьев и графов — например‚ поиск пути в файловой системе или обработка иерархических структур.
• Решение классических задач — такие как вычисление факториала‚ чисел Фибоначчи‚ расположение шахматных фигур и т.п.
• Декомпозиция сложных задач — разбиение большой задачи на повторяющиеся или схожие подзадачи.

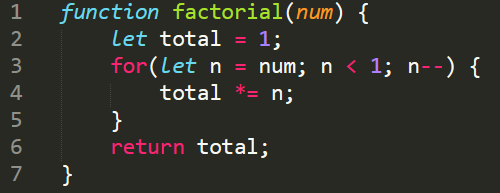
Пример: вычисление факториала с помощью рекурсии

---

Чтобы полностью понять‚ как работает рекурсия‚ обратимся к одному из классических примеров — вычислению факториала числа. Факториал числа n (обозначение: n!), это произведение всех натуральных чисел от 1 до n.

Определение факториала по рекурсии выглядит так: n! = n * (n-1)!‚ а для 0! = 1.

Код рекурсивной функции для вычисления факториала:

function factorial(n) {
 if (n === 0 || n === 1) {
 return 1; // базовое условие
 }
 return n * factorial(n ⎼ 1); // рекурсивный вызов
}

Преимущества и опасности рекурсии

---

Плюсы рекурсии

• Читаемость и краткость решения‚ особенно для задач‚ связанных с иерархическими структурами.
• Естественное решение сложных задач‚ связанных с разделением на подзадачи.
• Минимизация вложенных циклов‚ что часто делает код проще и понятнее.

Минусы и риски

• Высокий расход памяти из-за хранения стековых вызовов.
• Риск переполнения стека при слишком глубоких рекурсиях.
• Иногда итеративные методы оказываются более эффективными по скорости.

Как правильно использовать рекурсию

---

Для успешного применения рекурсии необходимо соблюдать несколько правил:

1. Определить четкое базовое условие. Без него функция станет бесконечно вызывать сама себя.
2. Передавать параметры‚ ведущие к базовому условию. Они должны приближать решение к завершению.
3. Оценивать глубину рекурсии. В сложных задачах желательно предусмотреть ограничение‚ чтобы не вызвать ошибку переполнения стека.
4. Использовать мемоизацию или другие техники оптимизации для повторяющихся вызовов с одинаковыми параметрами.

Рекурсия — мощный инструмент‚ если задача обладает естественной рекурсивной природой или сильно упрощается при разбиении. В противном случае лучше подумать о итеративных методах‚ которые часто более эффективны в плане использования ресурсов.

Практическое задание

Попробуйте самостоятельно реализовать функцию поиска файла в файловой системе с использованием рекурсии или написать рекурсивную функцию обхода структуры данных. Это отличный способ закрепить полученные знания и понять‚ как рекурсия работает «под капотом».

Часто задаваемые вопросы (FAQ)

Что такое база рекурсии?

Базовое условие — это ситуация‚ при которой рекурсивная функция перестает вызывать сама себя и начинает возвращать результат. Это необходимо для остановки бесконечных вызовов и обеспечения завершения алгоритма.