Итеративные реализации рекурсивных алгоритмов: Погружение в мир вычислений

Когда речь идет о программировании, мы часто сталкиваемся с двумя подходами к решению задач: рекурсивным и итеративным. Оба метода имеют свои преимущества и недостатки, и знание, как преобразовать рекурсивные алгоритмы в итеративные, может существенно улучшить нашу способность писать оптимизированный код. В этой статье мы исследуем ключевые аспекты итеративных реализаций рекурсивных алгоритмов, осветим их особенности и поделимся личным опытом, который поможет избежать распространенных ошибок при написании кода.

Мы обсудим, когда стоит использовать итерации вместо рекурсии, как оптимизировать код при помощи стека и очередей, а также приведем примеры перевода рекурсивных решений в итеративные. Мы надеемся, что эта статья поможет вам развить ваши навыки программирования и углубить понимание алгоритмов.

Что такое рекурсия и итерация?

Рекурсия – это метод, при котором функция вызывает саму себя для решения подзадачи. Этот подход позволяет решать сложные задачи, разбивая их на более простые. Например, классическим примером рекурсии является вычисление факториала числа, где

• Факториал тройки (3!) равен 3 * 2 * 1
• Факториал двойки (2!) равен 2 * 1

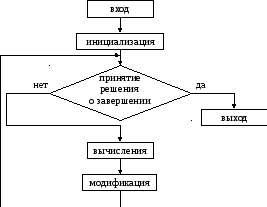
Итерация, с другой стороны, представляет собой процесс повторения определенного блока кода, пока не будет достигнуто желаемое состояние. Использование циклов, таких как for и while, позволяет программам контролировать повторяемость действий, что иногда очень важно для производительности.

В большинстве случаев, эти два подхода могут быть взаимозаменяемыми, но выбор между ними часто зависит от предпочтений программиста, характера задачи и требований к производительности.

Преимущества и недостатки рекурсии

Как и в любом подходе, у рекурсии есть свои достоинства и недостатки, которые следует учитывать.

• Преимущества:

• Сложные задачи можно решать проще, разбивая их на подзадачи.
• Код становится более читабельным и понятным.
• Снижается необходимость в промежуточных переменных.

Недостатки:

Рекурсия может привести к переполнению стека при глубоком вызове.

Иногда эффективность рекурсии может быть хуже, чем у итерации;

Рекурсивные алгоритмы могут быть сложнее для понимания начинающим программистам.

Когда стоит рассматривать итеративные реализации?

Итеративные алгоритмы следует рассматривать в нескольких ситуациях:

• Когда задача подразумевает большое количество вызовов функций и может вызвать переполнение стека.
• Когда необходимо оптимизировать алгоритм для повышения производительности.
• Когда требуется более прозрачное управление памятью.

На практике мы часто сталкивались с задачами, которые были проще и эффективнее реализованы именно с использованием итеративных подходов. Примеры таких задач включает в себя поиск в массиве, вычисление чисел Фибоначчи или обработку множества данных.

Преобразование рекурсии в итерацию: основные принципы

Для преобразования рекурсивного алгоритма в итеративный, нужно учитывать несколько ключевых моментов:

1. Использование стека или очереди для хранения промежуточных результатов.
2. Создание цикла, который будет обрабатывать элемент, пока все подзадачи не будут решены.
3. Работа с условием для выхода из цикла.

Рассмотрим подробнее, как это выглядит на практике.

Пример: Факторил

В качестве примера преобразования мы рассмотрим алгоритм вычисления факториала. Рекурсивная версия этого кода может выглядеть так:

function factorial(n) {
 if (n === 0) {
 return 1;
 }
 return n * factorial(n ⎻ 1);
}

Теперь давайте преобразуем этот код в итеративный:

function factorial(n) {
 let result = 1;
 for (let i = 1; i <= n; i++) {
 result *= i;
 }
 return result;
}

В этом случае мы упростили задачу, устранив необходимость в многократных вызовах функций и сделав алгоритм менее ресурсозатратным.

Использование стека и очереди при итеративных подходах

При разработке итеративных реализаций алигортмам часто полезно использовать стеки и очереди. Чтобы избежать многократных вызовов функций, мы можем "эмулировать" рекурсию с помощью явного управления стеком.

Для этого необходимо создать собственный стек, который будет содержать параметры запрашиваемых подзадач. Например:

function iterativeFactorial(n) {
 let stack = [];
 let result = 1;
 stack.push(n);
  while (stack.length > 0) {
 let current = stack.pop;
 if (current === 0) {
 continue;
 }
 result *= current;
 stack.push(current ⎯ 1);
 }
  return result;
}

Таким образом, мы достигаем результата, аналогично рекурсивному подходу, но без риска переполнения стека вызовов.

Часто встречающиеся ошибки при переходе от рекурсии к итерации

При преобразовании рекурсивных алгоритмов в итеративные версии мы часто сталкиваемся с определенными трудностями и ошибками. Вот некоторые из самых распространенных из них:

• Забывание о состоянии: Очень важно правильно вести учет промежуточного состояния при использовании итерации.
• Неправильный выход из цикла: Если не установить правильные условия выхода, программа может зациклиться.
• Неэффективное использование памяти: При использовании стека может потребоваться больше памяти.

Избежать этих ошибок можно лишь через практику и внимание к деталям.

Практические примеры других алгоритмов

Числа Фибоначчи

Алгоритм для вычисления чисел Фибоначчи также легко преобразуется из рекурсивного в итеративный. Рекурсивный алгоритм будет таким:

function fib(n) {
 if (n <= 1) {
 return n;
 }
 return fib(n ⎯ 1) + fib(n ⎯ 2);
}

И итеративный вариант:

function fib(n) {
 if (n <= 1) {
 return n;
 } let prev = 0;
 let curr = 1;
 for (let i = 2; i <= n; i++) {
 let temp = curr;
 curr = prev + curr;
 prev = temp;
 }
 return curr;
}

Чем больше значение n, тем более заметна разница в производительности между этими двумя подходами.

Таблица сравнения рекурсивных и итеративных алгоритмов

Критерий	Рекурсия	Итерация
Читаемость	Высокая	Зависит от реализации
Использование памяти	Высокое	Низкое
Производительность	Низкая для больших значений n	Высокая
Риск переполнения стека	Да	Нет

Итак, мы обсудили основные аспекты итеративных реализаций рекурсивных алгоритмов, их преимущества, недостатки и практические примеры. Мы провели ряд преобразований и рассмотрели способы избежать распространенных ошибок, которые могут быть связаны с этим процессом.

Итеративные алгоритмы становятся проще и эффективнее по мере улучшения навыков программиста, и поэтому мы рекомендуем практиковаться с разными задачами, чтобы закрепить понимание. Надеемся, что данная статья была вам полезна и вдохновит на дальнейшие эксперименты с алгоритмами!

Улучшение навыков в программировании требует постоянной практики, изучения новых технологий и алгоритмов, а также участия в различных проектах. Чтение книг, статей и участие в онлайн-курсах также значительно помогут развить ваши способности; Кроме того, практика решения алгоритмических задач на платформах, таких как LeetCode, Codewars, HackerRank и др., даст возможность закрепить теорию на практике.

Подробнее

Рекурсивные алгоритмы	Итеративные подходы	Оптимизация кода	Стек и очередь	Сравнение рекурсии и итерации
Функции на JavaScript	Алгоритмические задачи	Изучение программирования	Универсальные структуры данных	Кодирование и тестирование