Как работает сортировка деревом (AVL): полный разбор и практические советы

Когда мы говорим о структуре данных‚ которая способна обеспечить быстрый доступ‚ вставку и удаление элементов‚ на ум всегда приходят такие методы‚ как хэш-таблицы или деревья. Среди деревьев особого внимания заслуживает самобалансирующееся дерево AVL — удивительный алгоритм‚ способный поддерживать баланс и обеспечивать эффективность работы даже при больших объемах данных. Нам вместе предстоит понять‚ как работает этот механизм‚ почему он так полезен‚ и как его реализовать на практике.

---

Что такое дерево AVL и чем оно отличается от обычных деревьев поиска?

Дерево поиска — это структура‚ которая позволяет быстро находить‚ вставлять и удалять элементы. Однако‚ без специальных правил оно может превращаться в "заехавшую" в состояние‚ при котором поиск станет медленным. Например‚ если мы вставляем последовательные значения‚ дерево превращается в цепочку‚ что значительно увеличивает время поиска, как в списке.

Именно сюда приходит на помощь самобалансирующееся дерево AVL. Название происходит от инициалов из первых букв имен его изобретателей — Георгия Адельсона-Вельского и Евгения Ландиса. В отличие от обычных деревьев‚ дерево AVL при каждой вставке или удалении элементов стремится сохранить разницу высот левого и правого поддеревьев любого узла не более чем 1. Это состояние называется балансированным.

Преимущество такой структуры в том‚ что она гарантирует временную сложность операций поиска‚ вставки и удаления‚ которая равна O(log n)‚ что делает ее незаменимой при работе с большими наборами данных.

---

Основные понятия и принципы работы дерева AVL

Балансировка дерева

После каждой операции вставки или удаления нужно проверить баланс узлов. Если разница высот поддеревьев превышает 1‚ выполняются перестановки (или вращения)‚ возвращающие дерево в сбалансированное состояние.

Высота и балансировка

Высота узла — это максимальная глубина его поддеревьев‚ плюс один. В дереве AVL для каждого узла должна выполняться следующая формула:

| высота левого поддерева ౼ высота правого поддерева | ≤ 1

Типы вращений

Чтобы восстановить баланс‚ используются четыре типа вращений:

• Левое вращение (Left Rotation) — применяется при правомHeavy состоянии
• Правое вращение (Right Rotation), при левомHeavy состоянии
• Лево-правое вращение (Left-Right Rotation) — сложный случай‚ когда дерево тяжелее слева‚ а внутри — справа
• Право-левое вращение (Right-Left Rotation) — симметрично левому случаю‚ когда дерево тяжелее справа‚ а внутри — слева

Эти вращения позволяют всесторонне сохранять баланс и эффективность дерева.

---

Как происходит вставка элемента в дерево AVL

Пошаговое описание процесса вставки

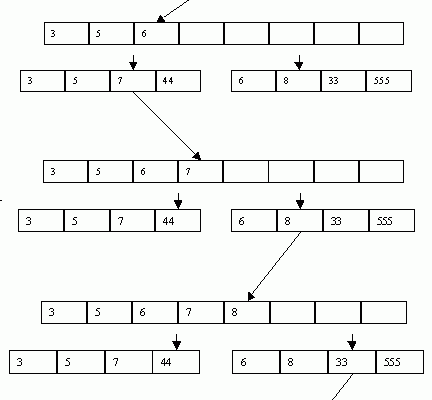
Рассмотрим‚ как осуществляется вставка элемента в дерево AVL на практике:

1. Производится стандартный поиск подходящего места для вставки по правилам двоичного поиска.
2. Находится подходящий лист или пустое место‚ и туда вставляется новый узел.
3. После вставки происходит проверка баланса. Если баланс сохранен — никаких действий не требуется.
4. Если баланс нарушен‚ выполняется серия вращений для восстановления равновесия.

Давайте посмотрим конкретный пример:

Шаг	Действие
1	Вставка элемента
2	Обновление высот узлов‚ на пути вверх
3	Проверка баланса узлов
4	Выполнение вращений при необходимости

Обобщая‚ вставка в AVL — это комбинация стандартной процедуры вставки и дополнительных шагов по сохранению баланса.

---

Удаление элемента из дерева AVL

Особенности удаления

Удаление элемента — более сложная операция‚ чем вставка‚ так как после удаления увеличивается вероятность нарушения баланса. В ходе удаления обнаруживается узел‚ который нужно убрать‚ а затем происходит замена‚ если это необходимо‚ и балансировка дерева аналогично вставке.

Пошаговая процедура

1. Нахождение узла для удаления.
2. Если у узла есть два потомка‚ находиться минимальный элемент в правом поддереве (или максимальный в левом)‚ и он заменяет удаляемый узел.
3. Удаление узла — либо листа‚ либо узла с одним потомком (сглаженная операция).
4. Обновление высот и балансировка вверх по дереву.

В этом процессе важна правильная реализация вращений для предотвращения деградации дерева.

---

Практическая реализация дерева AVL на примере кода

Основные функции

Рассмотрим основу реализации на языке программирования:

class Node {
 int key;
 int height;
 Node left;
 Node right;
}

public class AVLTree {
 private Node root;

 private int height(Node node) {
 return node == null ? 0 : node.height;
 }

 private int getBalance(Node node) {
 return node == null ? 0 : height(node.left) ⸺ height(node.right);
 }

 private Node rightRotate(Node y) {
 Node x = y.left;
 Node T2 = x.right;

 x.right = y;
 y.left = T2;

 y.height = Math.max(height(y.left)‚ height(y.right)) + 1;
 x.height = Math.max(height(x.left)‚ height(x.right)) + 1;

 return x;
 }

 private Node leftRotate(Node x) {
 Node y = x.right;
 Node T2 = y.left;

 y.left = x;
 x.right = T2;

 x.height = Math.max(height(x.left)‚ height(x.right)) + 1;
 y.height = Math.max(height(y.left)‚ height(y.right)) + 1;

 return y;
 }

 // Методы вставки‚ удаления и балансировки — далее...
}

Это базовая структура‚ которая демонстрирует‚ как реализовать вращения‚ поддержку высот и балансировку в дереве AVL.

---

Преимущества и недостатки дерева AVL

Преимущества

• Быстрый доступ к элементам благодаря логарифмической высоте дерева
• Эффективность при большом объеме данных
• Обеспечение сбалансированности автоматически при операциях вставки и удаления

Недостатки

• Сложность реализации по сравнению с простыми деревьями поиска
• Дополнительные операции по балансировке‚ что может влиять на скорость при небольших объемах данных
• Увеличение высоты дерева из-за вращений, иногда в некоторых случаях лучше использовать другие Self-balancing структуры‚ например‚ красно-черные деревья

---

Практические советы по использованию дерева AVL

Если вы собираетесь внедрять дерево AVL в свои проекты‚ важно учитывать несколько практических моментов. Во-первых‚ тщательно выбирайте подходящий язык программирования и библиотечные реализации‚ если таковые есть. Во-вторых‚ обязательно тестируйте операции вставки и удаления для обеспечения корректности работы и отсутствия ошибок в балансировке. И главное — на практике дерево AVL отлично подходит для систем с частыми операциями поиска и динамическими данными‚ где важна скорость выполнения.

Ответ очевиден — да! Благодаря своей способности поддерживать баланс при динамических операциях‚ дерево AVL остается одним из самых надёжных и быстрых методов организации данных. Его применение оправдано в базах данных‚ поисковых движках‚ системах с высокой нагрузкой‚ где критичны время поиска и вставки.

Конечно‚ для новичков реализация может показаться сложной‚ но освоение этой структуры открывает новые горизонты в понимании алгоритмов и успешной работы с большими объемами данных. Не бойтесь экспериментировать и внедрять‚ ведь именно практическое освоение технологических решений делает нас более профессиональными разработчиками.

Подробнее

балансировка дерева AVL	самобалансирующиеся деревья поиска	вращения в AVL деревьях	преимущества деревьев AVL	плюсы и минусы AVL
операции вставки в AVL	операции удаления из AVL	примеры кода AVL	использование дерева AVL	самобалансирующие деревья