Мастерство работы с двоичной кучей: как эффективно управлять данными и ускорить вычисления

Когда мы сталкиваемся с задачами обработки больших объемов данных или необходимостью быстрой сортировки и поиска минимальных или максимальных элементов‚ на ум приходят различные структуры данных. Одна из наиболее мощных и популярных — это двоичная куча. В этой статье мы подробно разберем‚ что такое двоичная куча‚ каким образом она строится и используется‚ а также изучим практические кейсы применения и оптимизации.

Многие считают‚ что структура данных — это что-то сложное и требующее глубоких знаний. Однако если подойти к этой теме системно и последовательно‚ то понимание двоичной кучи становится доступным даже для начинающих программистов. Мы подробно расскажем о её принципах‚ реализуем на практике и предложим рекомендации по использованию.

Что такое двоичная куча и зачем она нужна?

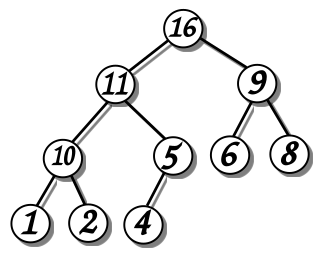
Двоичная куча — это специализированная структура данных‚ представляющая собой полное бинарное дерево‚ которое удовлетворяет свойству кучи: родительский элемент всегда больше или равен (в случае макс-кучи) или меньше или равен (в случае мин-кучи) своих дочерних элементов. Благодаря таким свойствам‚ двоичная куча позволяет эффективно получать и обновлять минимальные или максимальные значения.

Основные преимущества двоичной кучи — это быстрый доступ к минимальному или максимальному элементу и возможность легкого выполнения операций вставки и удаления; Эти свойства делают двоичную кучу незаменимой в реализациях алгоритмов‚ где важна скорость обработки данных‚ например‚ в алгоритмах поиска кратчайших путей‚ приоритетных очередях и средствам динамического распределения ресурсов.

Преимущества и области применения двоичной кучи

Рассмотрим основные достоинства этой структуры:

• Эффективность: операции вставки и удаления — всего O(log n); получение минимального или максимального — O(1).
• Простота реализации: реализуется легко с помощью массивов‚ что упрощает код и ускоряет работу.
• Гибкость: подходит как для реализации приоритетных очередей‚ так и для решения задач о поиске экстремумов в динамических данных.

Области применения двоичной кучи:

1. Реализация приоритетных очередей в операционных системах.
2. Алгоритм Хаффмана и кодирование данных.
3. Алгоритм Дейкстры для поиска кратчайших путей.
4. Обработка задач‚ связанных с динамическим распределением ресурсов.
5. В задачах сортировки‚ таких как пирамидальная сортировка (heap sort).

Структура и реализация двоичной кучи

Самая распространенная реализация двоичной кучи осуществляется на базе массива. В этом случае‚ структура дерева представляется в виде последовательного набора элементов:

Индекс элемента (i)	Родительский элемент	Левый ребенок	Правый ребенок
i	i/2	2i	2i+1

Это означает‚ что при хранении данных в массиве:

• Родитель для элемента с индексом i — это элемент с индексом floor(i/2).
• Левый ребенок, это элемент с индексом 2i.
• Правый ребенок — это элемент с индексом 2i + 1.

Основные операции и их алгоритмы

Рассмотрим подробно основные операции‚ которые выполняются над двоичной кучей:

1. Вставка элемента: Добавляем новый элемент в конец массива‚ затем «поднимаем его вверх» (heapify-up)‚ пока структура не восстановит свойство кучи.
2. Удаление корня (минимума или максимума): Замещаем корень последним элементом массива‚ а затем «просматриваем вниз» (heapify-down)‚ чтобы структура оставалась упорядоченной.
3. Построение кучи из массива: Можно построить двоичную кучу за O(n) методом «heapify»‚ начиная с нижних уровней дерева.

Пошаговая реализация вставки элемента

Для наглядности приведем базовый алгоритм вставки в двоичную кучу:

function insert(heap‚ element):
 heap.append(element)
 index = heap.size — 1
 while index > 0 and heap[parent(index)] > heap[index]:
 swap(heap[parent(index)]‚ heap[index])
 index = parent(index)

Этот алгоритм показывает‚ как происходит подъем нового элемента в дерево для восстановления свойства кучи. Аналогичным образом реализуются и другие операции.

Практические кейсы использования двоичной кучи

Двоичная куча применяется в множестве алгоритмов и решений реальных задач:

1. Приоритетные очереди: Обеспечивают быстрый доступ к элементам с высоким приоритетом‚ что важно в системах обработки задач.
2. Алгоритм Дейкстры: Использует двоичную кучу для эффективного выбора следующего минимального пути.
3. Пирамидальная сортировка (Heap Sort): Стандартный пример сортировки за эвристическую сложность O(n log n).
4. Алгоритм Хаффмана: Использует кучу для кодирования данных при сжатии.
5. Обработка потоков данных: В динамических системах‚ где данные поступают непрерывно‚ двоичная куча помогает быстро обновлять и получать важные показатели.

Как правильно выбирать и оптимизировать двоичную кучу?

Несмотря на универсальность и эффективность двоичной кучи‚ при работе с большими объемами данных важно учитывать нюансы:

• Размер памяти: Используйте динамическое выделение памяти под массивы или управляемые коллекции.
• Управление памятью: В некоторых языках важно избегать утечек и четко контролировать освобождение ресурсов.
• Оптимизация операций: В случаях частых вставок и удалений важно правильно выбрать структуру хранения и методы heapify.

Для повышения эффективности рекомендуется использовать адаптированные реализации‚ например‚ встроенные библиотеки или специально оптимизированный код.

Практические советы по использованию двоичной кучи

1. Перед началом работы четко определите‚ нужна ли мин-или макс-куча.
2. Для хранения данных используйте массивы‚ которые легко масштабировать.
3. Не забывайте про правильное обновление структуры после каждой операции.
4. Используйте встроенные функции или библиотеки для существенной экономии времени и усилий.

Двоичная куча — это мощный инструмент‚ который значительно ускоряет работу с большими объемами данных‚ позволяет реализовать приоритетные очереди и оптимизировать многие алгоритмы поиска и сортировки. Глубокое понимание её структуры‚ алгоритмов построения и обновления помогает писать эффективный и надежный код.

Главное — помнить о балансе между сложностью реализации и требованиями к скорости выполнения операций. А также важно не забывать о практическом применении‚ что позволяет максимально использовать потенциал двоичной кучи для решения ваших задач.

Подробнее

алгоритмы с двоичной кучей	реализация кучи на массивах	приоритетные очереди	сортировка heap sort	преимущества двоичной кучи
быстрая обработка данных	оптимизация вставки	использование в алгоритмах	эффективные структуры данных	репликация структур данных
строительство кучи с нуля	экономия памяти	приоритеты в обработке	упрощенные алгоритмы	динамическое обновление
использование внешней памяти	Обработка потоковых данных	применение в коммерческих задачах	обеспечение высокой скорости	современные методы