Почему Сортировка Шелла — это ваш лучший друг в программировании?

В мире алгоритмов и структур данных существует множество способов упорядочивания информации, но среди них мы считаем сортировку Шелла одной из наиболее интересных и эффективных. Она была названа в честь своего разработчика, Дональда Шелла, который предложил этот алгоритм в 1959 году. На протяжении многих лет различные программные приложения и проекты благодаря своей эффективности и простоте использования убирали его из забытья и снова выводили на передний план.

С этим алгоритмом мы сможем значительно сократить время, затрачиваемое на сортировку, благодаря гибкой и многослойной стратегии. При помощи сортировки Шелла мы можем упорядочить массивы данных быстро и без особых усилий, и именно в этом заключается её привлекательность как для новичков, так и для ветеранов программирования.

В этой статье мы погрузимся в мир сортировки Шелла, рассмотрим её принципы работы, различные последовательности шагов и выберем самые оптимальные из них для конкретных задач. Мы уверены, что после прочтения наши читатели не только лучше поймут данный алгоритм, но и смогут эффективно применять полученные знания на практике.

Что такое сортировка Шелла?

Сортировка Шелла является обобщением метода вставки, который мы могли бы использовать для упорядочивания данных. В отличие от простого метода вставки, который сравнивает только соседние элементы, сортировка Шелла сначала группирует элементы с определённым шагом, что позволяет значительно улучшить производительность.

Этот алгоритм сортирует элементы по более широким группам, которые постепенно уменьшаются, что позволяет переключаться на более строгую сортировку (обычно методом вставки), когда данные приближаются к отсортированному состоянию. Такой процесс значительно ускоряет общую сортировку, особенно для крупных массивов данных.

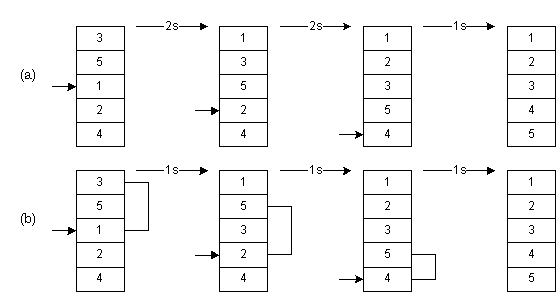
Как работает сортировка Шелла?

Все начинается с выбора начального значения для шага. На каждом этапе алгоритм будет брать элементы, которые находятся на расстоянии `h` друг от друга (где `h`, это шаг). Затем выполняется сортировка этих элементов, после чего шаг уменьшится, и процесс будет повторяться до тех пор, пока `h` не станет равным 1, то есть, пока не будет выполнена окончательная сортировка.

Это метод работает по следующему алгоритму:

1. Выберите шаг `h`, равный размеру массива, поделённый на 2.
2. Для каждого элемента массива с индексом `i`, начинающегося с `h`, выполняется сравнение с элементами на расстоянии `h` влево.
3. Если элементы не в порядке, они меняются местами.
4. Продолжайте процесс, уменьшая шаг, пока шаг не станет равным 1.
5. Выполните последнюю инкрементальную сортировку.

Выбор последовательности шагов

Важным аспектом сортировки Шелла является выбор последовательности шагов. Этим выбором можно управлять эффективностью сортировки. Разные последовательности шагов могут приводить к различной производительности алгоритма, и мы постараемся рассмотреть некоторые из наиболее популярных.

Последовательность Хиббарда

Одна из первых последовательностей, предложенных Хиббардом, выглядит следующим образом: 1, 3, 7, 15, 31 и т.д. Это мощная последовательность, которая предоставляет хороший компромисс между минимальной сложностью реализации и эффективностью.

Последовательность Праета

Последовательность Праета — это ещё один вариант, который имеет хорошую производительность. Она представлена в виде: 1, 4, 10, 23, 49, 109 и т.д.. Эта последовательность показывает лучшую производительность на больших массивах.

Последовательность Седжвика

Эта последовательность включает более сложные числа и даёт ещё большую эффективность. Последовательность может выглядеть следующим образом: 1, 5, 19, 41, 109, 209.

Сравнение последовательностей шагов

Последовательность	Формула	Преимущества	Недостатки	Типичные применения
Хиббард	2^k ⎯ 1	Простота реализации	Не всегда оптимальна для больших массивов	Общие сортировки
Праета	1, 4k + 1	Хорошая производительность	Сложность вычислений	Большие данные
Седжвик	Сложные числа	Максимальная эффективность	Сложность в реализации	Специфические задачи

Примеры и реализация в коде

Давайте рассмотрим, как мы можем реализовать сортировку Шелла на популярном языке программирования Python. Вот пример кода, который показывает, как работает этот алгоритм:

 
def shell_sort(arr):
 n = len(arr)
 gap = n // 2
 while gap > 0:
 for i in range(gap, n):
 temp = arr[i]
 j = i
 while j >= gap and arr[j — gap] > temp:
 arr[j] = arr[j — gap]
 j -= gap
 arr[j] = temp
 gap //= 2
 return arr

Пример использования
arr = [12, 34, 54, 2, 3]
print("Отсортированный массив:", shell_sort(arr))
 
 

Советы по оптимизации

Используйте следующие рекомендации, чтобы максимизировать эффективность сортировки Шелла:

• Точно выбирайте последовательность шагов, адаптируя её под свои данные.
• Пробуйте различные языки программирования для реализации алгоритма; производительность может отличаться.
• Используйте профилирование, чтобы выявить узкие места в вашем коде и внести улучшения.

Сортировка Шелла остаётся одним из наиболее эффективных методов упорядочивания массивов данных. Мы рассмотрели основные шаги, различные последовательности, их преимущества и недостатки, а также предложили оптимизацию кода. Несмотря на то, что существуют более современные алгоритмы сортировки, сортировка Шелла по-прежнему актуальна благодаря своей простоте, гибкости и эффективности.

Подробнее

Алгоритм сортировки Шелла	Оптимизация сортировки	Порядок сортировки	Сравнение алгоритмов сортировки	Практика программирования
Сортировка массивов	Программирование на Python	Сложность алгоритмов	Последовательности шагов	Учебник по сортировке