- Погружение в глубины: анализ рекурсии — что стоит знать каждому
- Что такое рекурсия: основные понятия и примеры
- Преимущества и недостатки рекурсии
- Преимущества использования рекурсии
- Недостатки рекурсии
- Типичные сценарии использования рекурсии
- Обход структур данных
- Обработка математических последовательностей
- Динамическое программирование
- Практические советы по использованию рекурсии
- Как правильно писать рекурсивные функции
- Когда лучше использовать итерацию вместо рекурсии
Погружение в глубины: анализ рекурсии — что стоит знать каждому
Когда мы говорим о программировании‚ алгоритмах или математике‚ одним из наиболее загадочных и в то же время мощных инструментов является рекурсия. Многие начинающие разработчики и даже опытные инженеры сталкиваются с этим понятием‚ не всегда полностью понимая его принципы и возможности. В этой статье мы совместно с вами разберемся‚ что такое рекурсия‚ как она работает‚ какие преимущества и сложности она приносит‚ а также научимся применять ее на практике.
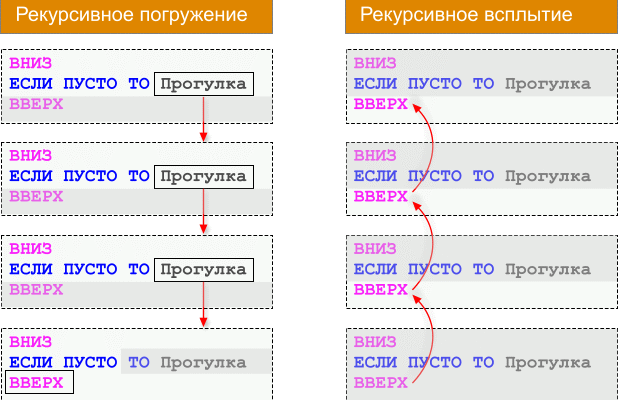
Рекурсия — это способ решения задач‚ при котором функция вызывает сама себя для решения подзадачи. В этих вызовах заложена идея деления сложной задачи на более простую‚ идентичную исходной‚ с целью упростить вычисление. Впрочем‚ чтобы реализовать рекурсию правильно‚ необходимо внимательно контролировать базовые случаи‚ предотвращая бесконечные циклы.
Что такое рекурсия: основные понятия и примеры
В основном‚ рекурсия — это метод‚ при котором задача разбивается на более мелкие‚ простые части‚ и решение каждой части происходит через вызов той же функции‚ примененной к подзадаче. Самое важное условие — наличие базового случая‚ который завершает цепочку вызовов и предотвращает вечную рекурсию.
Рассмотрим классический пример — вычисление факториала числа:
| Пример | Объяснение |
|---|---|
| Факториал(н) | Это произведение всех натуральных чисел от 1 до н. Например‚ 5! = 1×2×3×4×5. |
| Рекурсивное определение | n! = n × (n-1)! при n > 1‚ и 1! = 1, базовый случай. |
| Код функции на Python | def factorial(n): if n == 1: return 1 else: return n * factorial(n ⎼ 1) |
Здесь мы видим две важные части: базовый случай (n==1) и рекурсивный вызов (n * factorial(n-1)). Эта цепочка продолжается‚ пока не достигнет базового случая‚ тем самым завершив вычисление.
Преимущества и недостатки рекурсии
Преимущества использования рекурсии
- Естественное решение сложных задач — в некоторых случаях рекурсия позволяет выразить алгоритм очень компактно и понятно‚ например‚ при обходе деревьев или графов.
- Облегчение кода — для задач‚ где проблема по сути сводится к повторяющимся одинаковым операциям‚ рекурсия зачастую делает код более читабельным.
- Глубина анализа, помогает разобраться в сложных структурных данных‚ таких как деревья‚ списки‚ графы.
Недостатки рекурсии
- Высокое использование памяти — каждый вызов функции создает отдельный стек вызовов‚ что в некоторых случаях может привести к переполнению стека (StackOverflow).
- Неряшливость в реализации — неправильная постановка базового случая или отсутствие его может привести к бесконечному вызову.
- Производительность, в сравнении с итерациями рекурсия часто менее эффективна‚ особенно если повторные вычисления не оптимизированы с помощью мемоизации.
Типичные сценарии использования рекурсии
Рекурсия нашла свое применение во многих алгоритмических задачах. Ниже представлены наиболее часто встречающиеся сценарии‚ которые практически невозможно решить без использования рекурсии или которые существенно выигрывают в понятности и краткости именно с ее помощью.
Обход структур данных
Обход деревьев‚ графов‚ списков — это классическая область‚ где рекурсия проявляется наиболее ярко.
- Обход дерева в глубину (DFS) — при посещении узла мы вызываем обход для его дочерних элементов.
- Обход дерева в ширину (BFS) — чаще реализуется через очередь‚ но также связанные с рекурсией задачи.
Обработка математических последовательностей
Факториалы‚ числа Фибоначчи‚ числа Тарту и другие — рекурсия часто используют для их вычисления.
Динамическое программирование
Рекурсия‚ в связке с мемоизацией или табуляцией‚ позволяет эффективно решать задачи с повторяющимисяподзадачами‚ такие как долгосрочные планирования‚ оптимизации маршрутов и т.д.
Практические советы по использованию рекурсии
Как правильно писать рекурсивные функции
Чтобы избежать распространенных ошибок и сделать код максимально надежным‚ необходимо соблюдать несколько важных правил:
- Обязательно определите базовый случай. Он должен быть ясным и достижимым. Иначе функция зациклится в бесконечном вызове.
- Минимизируйте глубину рекурсии. Постарайтесь разбивать задачи так‚ чтобы глубина вызовов не превышала допустимых лимитов.
- Используйте мемоизацию для сохранения результатов уже посчитанных подзадач‚ чтобы избежать повторных вычислений.
- Проверяйте параметры функции. Они должны быть корректными и предусматривать все возможные сценарии.
Когда лучше использовать итерацию вместо рекурсии
Несмотря на привлекательность рекурсии‚ иногда более рационально применять итерационные подходы:
- При глубине рекурсии‚ превышающей лимит стека.
- Когда важна максимальная производительность.
- При необходимости избежать возможных ошибок переполнения стека.
В таких случаях обычно используют циклы (for‚ while)‚ которые позволяют контролировать выполнение гораздо лучше и потребляют меньше памяти.
Рекурсия — это мощный инструмент‚ который при правильном использовании способен значительно упростить решение сложных задач и улучшить читаемость кода. Однако важно помнить о возможных ограничениях и рисках‚ связанных с переполнением стека и низкой производительностью.
Если вы только начинаете овладевать этим подходом‚ рекомендуется сначала разобраться с простыми примерами и постепенно переходить к более сложным ситуациям. Также не забывайте о таких приёмах‚ как мемоизация‚ это значительно ускорит вычисления и сделает рекурсию более эффективной.
Обязательно экспериментируйте с задачами‚ которые можно решить через рекурсию‚ — так вы лучше почувствуете её плюсы и минусы‚ а также научитесь правильно её применять.
Вопрос: Почему рекурсия иногда считается сложной для понимания и реализации‚ и как этого избегать?
Рекурсия часто воспринимается как сложная из-за своей концептуальной особенности, функции‚ вызывающей саму себя‚ что может казаться противоинтуитивным‚ особенно для новичков. Она требует понимания идеи остановочного условия и правильной постановки базового случая. Часто начинающие делают ошибку‚ не определяя базовый случай или неправильно его реализуя‚ что приводит к бесконечным вызовам и ошибкам. Чтобы избежать этих проблем‚ рекомендуется сначала изучать рекурсию на простых примерах‚ понимать‚ как работает стек вызовов‚ и обязательно тестировать базовые случаи. Также полезно визуализировать процесс вызовов‚ например‚ рисовать деревья рекурсии‚ что поможет лучше понять логику и структуру выполнения.
Подробнее
| Учимся быстро считать рекурсию | Обучение рекурсивным вызовам | Обход деревьев рекурсией | Динамическое программирование и рекурсия | Мемоизация в рекурсии |
| рекурсия и стека вызовов | пример рекурсивных функций | обход дерева рекурсией | использование мемоизации | оптимизация рекурсии |