Сортировка деревом: Погружаемся в мир AVL-деревьев

В мире алгоритмов и структур данных есть множество способов упорядочивания информации․ Однако, когда речь заходит о быстром и эффективном поиске, внесении и удалении данных, на ум приходит AVL-дерево․ Это структура данных, которая поддерживает элементы в отсортированном порядке, позволяя выполнять операции поиска, добавления и удаления за логарифмическое время․ В этой статье мы обсудим, что представляет собой AVL-дерево, как оно работает, и какие преимущества предлагает․

AVL-деревья, названные в честь своих создателей Георга Авлериха и Валентина Ландиса, предоставляют оптимальный способ хранения и управления отсортированными данными․ Их основная особенность заключается в использовании механизма балансировки, что гарантирует, что высота дерева всегда остается логарифмической относительно количества узлов, обеспечивая высокую скорость выполнения операций․ Эта балансировка убережёт нас от проблем, связанных с деградацией производительности, присущей простым бинарным деревьям․

Что такое AVL-дерево?

AVL-дерево является разновидностью бинарного дерева поиска, удовлетворяющего специальному критерию балансировки․ В основе AVL-дерева лежит принцип, что для каждого узла высота его левого поддерева и высота его правого поддерева может различаться не более чем на один․ Это значит, что AVL-дерево всегда имеет сбалансированную структуру, что является его главной силой․

Основные характеристики AVL-деревьев:

• Каждый узел дерева содержит ключ (данные) и ссылки на левое и правое поддеревья․
• Для каждого узла высота левого и правого поддерева отличается не более чем на единицу․
• Операции поиска, вставки и удаления выполняются за O(log n) времени, где n — количество узлов в дереве․

Как работает AVL-дерево?

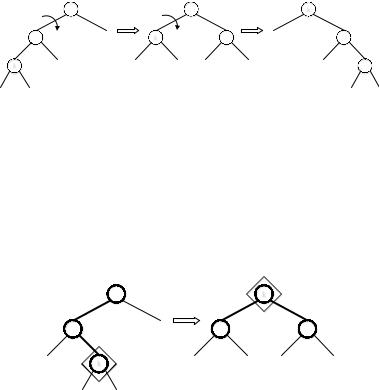
Основная идея работы AVL-дерева заключается в том, что после выполнения операций вставки или удаления происходит переупорядочивание узлов для поддержания свойства балансировки․ Если во время вставки или удаления высота левого и правого поддеревьев нарушается, то дерево необходимо сбалансировать с помощью специальных вращений․

Существует несколько случаев, когда может произойти дисбаланс:

• Левое левое вращение (LL) — происходит, когда новый узел добавляется в левое поддерево левого узла;
• Правое правое вращение (RR), происходит, когда новый узел добавляется в правое поддерево правого узла․
• Левое правое вращение (LR) — происходит, когда новый узел добавляется в правое поддерево левого узла․
• Правое левое вращение (RL), происходит, когда новый узел добавляется в левое поддерево правого узла․

Алгоритмы балансировки

Процесс балансировки AVL-дерева включает в себя множество этапов․ Сначала мы должны определить высоту узлов, чтобы понять, есть ли необходимость в балансировке․ Если разница в высоте между левым и правым поддеревом превышает 1, нужно выполнить балансировку․

Ниже представлена таблица, описывающая различные случаи балансировки:

Случай	Описание	Тип вращения
LL	Новый узел добавляется в левое поддерево	Правое вращение
RR	Новый узел добавляется в правое поддерево	Левое вращение
LR	Новый узел добавляется в правое поддерево левого узла	Левое-правое вращение
RL	Новый узел добавляется в левое поддерево правого узла	Правое-левое вращение

Примеры работы с AVL-деревьями

Чтобы лучше понять, как работает AVL-дерево, давайте рассмотрим два примера: добавление и удаление узлов․

Добавление узлов

Предположим, мы начинаем с пустого дерева и поочередно добавляем значения: 10, 20, 30․ После добавления 10 и 20, дерево выглядит как:

• 10

• 20

Затем, при добавлении 30, дерево становится несбалансированным, и мы должны выполнить балансировку (RR вращение):

• 20

• 10
• 30

Удаление узлов

Теперь рассмотрим, что произойдет при удалении узла․ Например, если мы удалим 10 из дерева, то получится:

• 20

• 30

В этом случае дерево остается сбалансированным, и дополнительных действий по балансировке не требуется․

Преимущества и недостатки AVL-деревьев

Как и любая другая структура данных, AVL-деревья имеют свои преимущества и недостатки․

Преимущества

• Быстрый доступ к данным благодаря поддержанию структуры деревьев в сбалансированном состоянии․
• Высокая скорость выполнения операций поиска, вставки и удаления․
• Гарантированное логарифмическое время выполнения операций․

Недостатки

• Сложность реализации из-за необходимости поддержания балансировки после операций․
• Повышенная затрата ресурсов на операции вставки и удаления из-за возможных вращений․

Где используются AVL-деревья?

AVL-деревья находят широкое применение в различных областях, где требуется быстрая обработка данных․ Они используются в системах баз данных, в кодировках информации, в реализации различных алгоритмов, связанных с упорядочиванием данных и их поиском․

Примеры применения

• Хранение данных в системах управления базами данных․
• Реализация кэшей для быстрого доступа к данным․
• Обработка запросов в веб-приложениях и API․

AVL-деревья представляют собой мощный инструмент для хранения и обработки данных․ Их сбалансированная структура позволяет эффективно выполнять операции поиска, добавления и удаления․ Несмотря на определенные недостатки, связанные с реализацией и управлением, их преимущества делают их идеальным выбором для многих современных приложений․ В процессе нашего изучения мы погрузились в тонкости работы данной структуры и рассмотрели, как AVL-деревья могут помочь в упрощении и ускорении алгоритмов обработки данных․

Основная роль AVL-деревьев в современной информатике заключается в их способности поддерживать упорядоченные данные, обеспечивая быстрый доступ и манипуляции с ними․ Они идеально подходят для приложений, требующих частого изменения данных, например, в базах данных и кэшах․ Благодаря высокой эффективности, такие структуры становятся незаменимыми в рамках многих других алгоритмов и приложений․

Подробнее

Компьютерные структуры данных	Алгоритмы поиска	Деревья поиска	Балансировка деревьев	Структуры данных в Python
Основы AVL-деревьев	Производительность операций	Сравнение деревьев	Алгоритмы сортировки	Общие принципы работы с деревьями