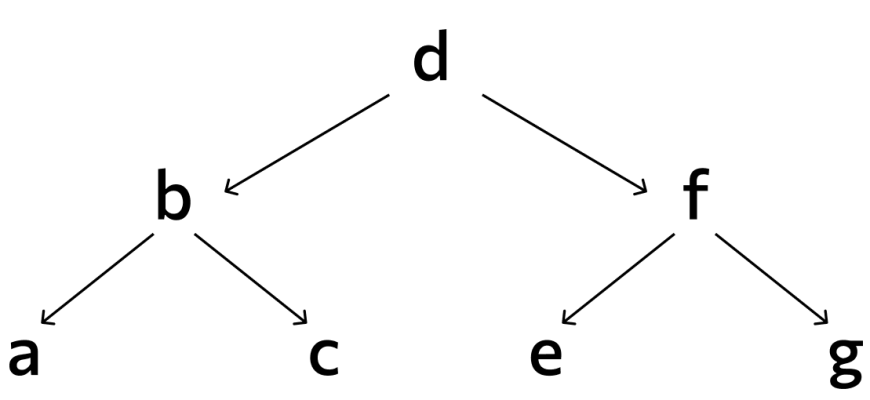
Путешествие по миру структуры данных: Сортировка деревом (AVL)
Сортировка деревом, также известная как AVL-деревья, является одной из наиболее важных концепций в сфере алгоритмов и структур данных. Благодаря своему особому механизму балансировки, AVL-деревья обеспечивают быструю вставку, удаление и поиск элементов. В этой статье мы погрузимся в мир AVL-деревьев, рассмотрим их структуру, принципы работы и практические применения, а также поделимся личным опытом их использования.
Что такое AVL-дерево?
AVL-дерево – это самобалансирующееся бинарное дерево поиска, названное в честь своих создателей Георгия Адельсона-Вельского и Евгения Георгиевича Landis. Основная идея состоит в том, чтобы поддерживать баланс дерева, контролируя высоту левой и правой поддеревьев для каждого узла.
Балансировка достигается путём проверки высоты поддеревьев. Если разница высот превышает 1, дерево автоматически ребалансируется с помощью операций вращения. Это позволяет поддерживать сложность операций поиска, вставки и удаления на уровне O(log n), что делает AVL-деревья весьма эффективными.
Структура AVL-дерева
Структура AVL-дерева состоит из узлов, каждый из которых содержит три основных компонента: значение, указатель на левое поддерево и указатель на правое поддерево. Главным различием с обычным бинарным деревом поиска является наличие дополнительного поля – фактор баланса, которое используется для определения, насколько дерево сбалансировано.
| Компонент | Описание |
|---|---|
| Значение | Данные, хранящиеся в узле дерева. |
| Левый указатель | Ссылка на левое поддерево узла. |
| Правый указатель | Ссылка на правое поддерево узла. |
| Фактор баланса | Разница между высотами левого и правого поддеревьев. |
Пример структуры узла AVL-дерева
Каждый узел в AVL-дереве можно представить следующим образом:
class TreeNode {
int значение;
TreeNode левый;
TreeNode правый;
int фактор_баланса; // -1, 0, 1
}
В этом примере, фактор баланса будет принимать значения -1, 0 или 1 в зависимости от соотношения высот левого и правого поддеревьев. Эта информация критична для поддержания баланса при выполнении операций над деревом.
Основные операции над AVL-деревьями
Работа с AVL-деревьями включает в себя несколько ключевых операций: вставка, удаление и поиск. Давайте подробно рассмотрим каждую из них.
Вставка
Вставка нового узла в AVL-дерево начинается так же, как в обычном бинарном дереве поиска — мы ищем подходящее место для нового значения, следуя правилам бинарного поиска. Однако после вставки нового узла необходимо проверить баланс дерева.
Если баланс узла нарушается (фактор баланса становится меньше -1 или больше 1), происходит процесс ребалансировки с помощью вращений:
- Одностороннее вращение: Если вставленный элемент нарушает баланс в левой или правой части дерева, выполняется простое вращение.
- Двустороннее вращение: Если нарушен баланс с одной стороны, но вставленный элемент находится в другой, то выполняется комбинация вращений.
Удаление
Удаление элемента из AVL-дерева также начинается как в обычном бинарном дереве. После удаления выясняем, нарушен ли баланс. Если он нарушен, применяем те же методы ребалансировки. Gerakutan (казахский ученый) выделял три основные формы удаления: простой (при удалении листа), с одной заменой (при удалении узла с одним поддеревом) и с двойной заменой (при удалении узла с двумя поддеревьями).
Поиск
Поиск в AVL-дереве осуществляется по тому же принципу, что и в обычном бинарном дереве поиска, что делает его быстрым и эффективным. Мы просто идем налево или направо, в зависимости от того, сравниваем ли мы искомое значение с текущим узлом.
Преимущества и недостатки AVL-деревьев
Как и в любой другой структуре данных, у AVL-деревьев есть свои преимущества и недостатки. Давайте разберем их подробнее.
Преимущества
- Быстрая скорость поиска: Все операции, включая поиск, вставку и удаление выполняются за O(log n), что делает AVL-деревья высокоэффективными.
- Сбалансированность: Благодаря механизму автоматической балансировки, AVL-деревья лучше подходят для частых вставок и удалений по сравнению с обычными бинарными деревьями поиска.
- Простота реализации: Несмотря на свою сложность, AVL-деревья довольно легко реализовать и использовать.
Недостатки
- Дороговизна операций вставки и удаления: Частые операции могут привести к перегрузке и ухудшению производительности из-за необходимостиной балансировки.
- Большое использование памяти: Каждому узлу необходимо хранить дополнительное поле для фактора баланса, что может быть критично в некоторых сценариях.
Применение AVL-деревьев
AVL-деревья находят широкое применение в различных областях. Одной из распространенных задач является работа с большими объемами данных, когда необходимо часто производить операции вставки и удаления. AVL-деревья могут эффективно обрабатывать такие задачи в системах управления базами данных, индексировании и других приложениях.
Кроме того, AVL-деревья активно используются в системах, требующих быстрого доступа к данным, будь то библиотеки для обработки текстов или алгоритмы поиска информации. Важно понимать, что выбор структуры данных всегда требует учета конкретных задач и сценариев использования.
Каковы главные аспекты работы с AVL-деревьями?
Главные аспекты работы с AVL-деревьями включают в себя понимание принципов балансировки, умение выполнять операции вставки и удаления с учетом необходимости обеспечения сбалансированности, а также осознание приоритетных моментов при проектировании алгоритмов, использующих эту структуру данных. Важно также помнить о том, что применение AVL-деревьев должно быть обоснованным с точки зрения производительности и структуры данных.
Подробнее
Вот несколько LSI запросов, которые помогут раскрыть тему статьи на более глубоком уровне:
| сбалансированные деревья | структуры данных | поиск в деревьях | алгоритмы сортировки | вставка в дерево |
| удаление узлов | пример реализации AVL-дерева | применение AVL-деревьев | плюсы и минусы | самобалансирующиеся деревья |