Radix Sort: Погружаемся в Мир Быстрых и Эффективных Сортировок на Основе Разрядов

В мире алгоритмов сортировки существует множество методов‚ каждый из которых подходит для определенных задач и условий. Среди них особое место занимает Radix Sort — алгоритм‚ который‚ несмотря на свою простоту и необычную концепцию‚ способен удивительно быстро справляться с большими объемами данных. В этой статье мы подробно рассмотрим сортировку по разрядам — MSD Radix Sort‚ разберемся‚ как она работает‚ в чем ее преимущества и слабые стороны‚ и почему она заслужила место в арсенале любого программиста.

Что такое Radix Sort и чем он отличается от других методов сортировки?

Пожалуй‚ одним из самых интересных аспектов Radix Sort является его концепция: в отличие от традиционных методов‚ таких как Quick Sort или Merge Sort‚ он не работает путём сравнения элементов. Вместо этого‚ алгоритм сортирует числа по разрядам — начиная с самых младших или самых старших — и постепенно получает полностью отсортированный массив.

Это принципиальное отличие делает Radix Sort особенно эффективным при обработке больших объемов целых чисел или строк‚ где значения имеют одинаковую длину или хорошо структурированы. Вместо сложных сравнений‚ алгоритм использует вспомогательные структуры — обычно очереди или временные массивы — для организации элементов по разрядам.

История появления и развитие Radix Sort

Истоки Radix Sort уходят в далекое прошлое‚ в XIX век‚ когда математики и инженеры начали искать быстрые методы организации данных. Впервые идеи‚ похожие на современные подходы к сортировке по разрядам‚ были описаны еще в 1887 году‚ однако широкое распространение получили лишь в XX веке.

С тех пор алгоритм улучшался и модернизировался. Сегодня он используется в различных сферах — от баз данных до систем обработки больших данных — благодаря своей скорости и эффективности при наличии правильных условий.

Механизм работы алгоритма MSD Radix Sort

Прежде чем углубиться в технические детали‚ важно понять основной принцип работы MSD (Most Significant Digit) Radix Sort — сортировка по наиболее значимому разряду. Этот подход подразумевает последовательно обработку цифр или символов‚ начиная с самого старшего‚ и далее по убыванию.

Общий алгоритм можно представить следующим образом:

1. Определение максимальной длины элемента – определяем самое длинное число или строку.
2. Обработка разрядов по убыванию – начиная с наиболее значимого разряда‚ сортируем элементы‚ распределяя их по временным контейнерам.
3. Рекурсивное повторение – для каждого контейнера повторяем сортировку по следующему разряду‚ пока не пройдет весь диапазон.

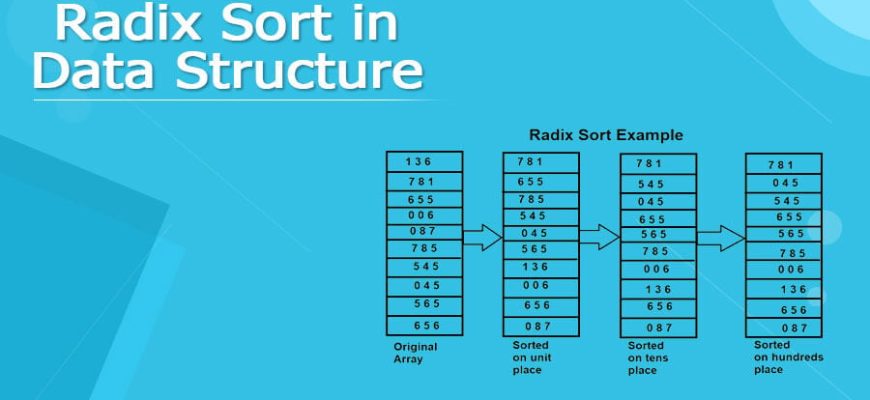
Рассмотрим пример с числами‚ чтобы понять этот процесс более наглядно:

Число	Разрядность (слева направо)
958	Местоположение 1: ‘9’
347	Местоположение 2: ‘3’
125	Местоположение 3: ‘1’
780	Местоположение 4: ‘7’

Начинаем сортировать числа‚ начиная с самой старшей цифры (разряда). После перераспределения по корзинам‚ получаем упорядоченный массив по этим разрядам‚ и затем продолжаем по следующему.

Шаги сортировки MSD Radix Sort

Для лучшего понимания переработаем алгоритм в несколько этапов:

• Определение диапазона: находим максимальное число и определяем его длину (или максимально возможное число символов для строк).
• Итеративная обработка разрядов: начиная с наиболее старшего‚ распределяем элементы по корзинам‚ основываясь на текущем разряде.
• Объединение и повторение: собираем элементы из корзин и повторяем процесс для следующего по значимости разряда.

Важно отметить‚ что при использовании базы (например‚ десятичной — 10)‚ мы всегда имеем фиксированный диапазон возможных значений разрядов.

Преимущества и слабости MSD Radix Sort

Каждый алгоритм имеет свои сильные и слабые стороны‚ и Radix Sort, не исключение. Рассмотрим подробно‚ почему его стоит выбрать в определённых ситуациях‚ и когда лучше отказаться от него.

Преимущества алгоритма

• Высокая скорость: в случае с большими массивами чисел или строк он показывает удивительно быструю работу‚ часто превосходящую сравнивающие сорта.
• Линейная сложность: при ограниченном диапазоне разрядов TStringSort работает за O(n * k)‚ где n — количество элементов‚ а k — длина элемента (например‚ число цифр);
• Не зависит от сравнений: не выполняет сравнений элементов‚ что снижает вероятность худших сценариев.

Недостатки алгоритма

• Зависимость от длины элементов: при очень больших длинах строк или чисел эффективность снижается.
• Дополнительная память: требует временных структур для хранения элементов по разрядам‚ что увеличивает объем используемой памяти.
• Работает в основном с целыми числами или фиксированной длины строками: неэффективен для произвольных данных без определенной структуры разрядов.

Реальные кейсы использования MSD Radix Sort

Несмотря на свои ограничения‚ Radix Sort активно применяется в различных областях. Ниже приведены наиболее популярные сценарии‚ где его применение оправдано и даже необходимо.

• Обработка больших объемов числовых данных — базы данных‚ поисковые системы.
• Сортировка строк фиксированной длины, например‚ коды товаров‚ идентификаторы‚ строки с одинаковым количеством символов.
• Эффективность в системах‚ где важна скорость и предсказуемость — системное программирование‚ быстродействующие системы обработки данных.

Практический пример реализации MSD Radix Sort на Python

Для закрепления материала рассмотрим простую реализацию алгоритма. Ниже приведена примерная версия сортировки для чисел на Python‚ использующая подход MSD.

def counting_sort_for_digit(arr‚ digit):
 """Сортировка по конкретному разряду (digit) с помощью подсчета."""
 count = [0] * 10
 output = [0] * len(arr)

 for num in arr:
 index = (num // digit) % 10
 count[index] += 1

 for i in range(1‚ 10):
 count[i] += count[i ⏤ 1]

 i = len(arr) — 1
 while i >= 0:
 index = (arr[i] // digit) % 10
 output[count[index] ⏤ 1] = arr[i]
 count[index] -= 1
 i -= 1
 return output

def radix_sort_msd(arr‚ max_digit):
 """Рекурсивная сортировка по наиболее значимому разряду."""
 if max_digit == 0:
 return arr

 arr = counting_sort_for_digit(arr‚ max_digit)
 # Для MSD сортировки надо запускать для каждого разряда отдельно
 # В этом общем виде можно дополнительно разделить на поразрядную обработку по уровням

 # В более сложных реализациях применяется рекурсия и обход по разрядам
 return arr


Пример использования
numbers = [958‚ 347‚ 125‚ 780‚ 663‚ 42‚ 111]
max_num = max(numbers)
max_digits = len(str(max_num))
sorted_numbers = radix_sort_msd(numbers‚ 10 ** (max_digits — 1))
print(sorted_numbers)

Эта реализация — лишь краткое введение. Для полноценной MSD сортировки потребуется более сложная рекурсивная обработка‚ однако она показывает основы концепции.

Подведение итогов

Итак‚ Radix Sort‚ особенно его тип MSD‚ представляет собой мощный инструмент для быстрого и эффективного упорядочивания чисел и строк‚ когда данные имеют структуру разрядов. Несмотря на свои ограничения‚ он отлично подходит для обработки больших объемов данных‚ особенно при работе с фиксированной длиной элементов. Понимание принципов его работы поможет сделать ваше программирование более гибким и эффективным‚ расширить горизонты в системах обработки данных и фундаментальных алгоритмах.

Подробнее

a href=#>Сортировка по разрядам	a href=#>Алгоритмы сортировки	a href=#>Сложность Radix Sort	a href=#>Реализация Radix Sort	a href=#>Недостатки Radix Sort
a href=#>Примеры сортировки Radix	a href=#>Плюсы и минусы MSD Radix	a href=#>Область применения Radix	a href=#>История разработки Radix	a href=#>Лучшие практики использования Radix