Рекурсия в программировании: Погружение в мир самоссылающихся алгоритмов

Когда речь заходит о рекурсии, многие программисты сразу же вспоминают о классической задаче Фибоначчи, где последовательность начинается с 0 и 1, а каждый последующий элемент равен сумме двух предыдущих․ Мы погружаемся в этот удивительный мир, где программист становится частью процесса самоссылающегося алгоритма․ Рекурсия не только является мощным инструментом, но и открывает двери в новое понимание решений задач․ В данной статье мы рассмотрим, что такое рекурсия, какие типы рекурсии существуют, а также примеры её применения в реальной жизни․

Мы уверены, что изучение рекурсии значительно расширяет понимание алгоритмических решений․ Это понятие часто вызывает путаницу, особенно у начинающих программистов․ Часто задаваясь вопросом: «Чем же полезна рекурсия?», мы начнем с того, что рассмотрим сам принцип и его важнейшую роль в программировании․

Что такое рекурсия?

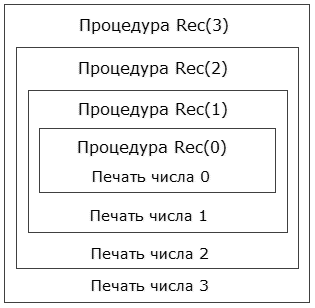
Рекурсия — это процесс, при котором функция вызывает сама себя․ Основным принципом работы рекурсивной функции является наличие базового случая, при котором происходит завершение рекурсивных вызовов․ Это предотвращает бесконечную рекурсию и гарантирует, что программа в конечном итоге завершится․

На первый взгляд, может показаться, что использование рекурсии, это излишняя сложность․ Однако, как только мы начинаем анализировать различные алгоритмы, становится очевидным, что рекурсивные методы способны значительно упростить решения многих задач․ Давайте разберем некоторые основные аспекты рекурсии, чтобы понять, как и когда её использовать․

Основные характеристики рекурсивных алгоритмов

Рекурсивные алгоритмы имеют несколько ключевых характеристик:

• Базовый случай: это условие, при котором рекурсивные вызовы прекращаются․
• Рекурсивный случай: это условие, при котором функция вызывает саму себя․
• Стек вызовов: каждый рекурсивный вызов добавляется в стек памяти, что может привести к переполнению стека, если не учитывать базовый случай․

Понимание этих характеристик поможет нам избежать распространенных ошибок, таких как бесконечная рекурсия и переполнение стека, что является важным аспектом анализа рекурсии․

Типы рекурсии

Рекурсия можно классифицировать по нескольким критериям․ Рассмотрим наиболее распространенные типы:

Прямая рекурсия

Прямая рекурсия — это когда функция вызывает саму себя․ Примером может служить вычисление факториала числа:

function factorial(n) {
 if (n === 0) return 1; // базовый случай
 return n * factorial(n ⎯ 1); // рекурсивный случай
}

Косвенная рекурсия

Косвенная рекурсия происходит, когда функция A вызывает функцию B, которая, в свою очередь, вызывает функцию A․ Примером может быть следующая пара функций:

function funcA(n) {
 if (n > 0) {
 funcB(n ‒ 1); // вызов функции B
 }
}

function funcB(n) {
 if (n > 0) {
 funcA(n ‒ 1); // вызов функции A
 }}

Примеры применения рекурсии

Мы можем наблюдать, как рекурсия используется в различных алгоритмах и задачах․ Рассмотрим несколько популярных примеров:

Поиск в деревьях

Деревья — это структура данных, которая может быть эффективно обходена с помощью рекурсии․ Например, для обхода бинарного дерева мы можем использовать рекурсивный алгоритм:

function traverseTree(node) {
 if (node) {
 console․log(node․value); // обработка текущего узла
 traverseTree(node․left); // рекурсивный вызов для левого поддерева
 traverseTree(node․right); // рекурсивный вызов для правого поддерева
 }
}

Сортировка массивов

Алгоритм быстрой сортировки (Quicksort) также использует рекурсию для разбиения массива на меньшие подмассивы․ Рассмотрим, как это выглядит:

function quicksort(array) {
 if (array․length <= 1) return array; // базовый случай
 const pivot = array[array․length ⎯ 1]; // выбор опорного элемента
 const left = array․filter(x => x < pivot);
 const right = array․filter(x => x > pivot);

 return [․․․quicksort(left), pivot, ․․․quicksort(right)]; // рекурсивный случай
}

Эти примеры показывают, как рекурсия позволяет нам решать сложные задачи, упрощая реализацию кода․

Преимущества и недостатки рекурсии

Мы должны помнить, что у рекурсии есть как преимущества, так и недостатки․ Давайте рассмотрим их подробнее․

Преимущества

• Краткость кода: Рекурсивные функции часто короче и понятнее, чем их итеративные аналоги․
• Удобство в решении сложных задач: Многие алгоритмические задачи, такие как обход деревьев и графов, резко упрощаются при использовании рекурсии․
• Естественная модель: Рекурсивные функции часто более наглядны и легче воспринимаются․

Недостатки

• Переполнение стека: При глубокой рекурсии может произойти переполнение стека вызовов, что приведет к ошибке․
• Производительность: Рекурсивные функции могут быть менее эффективными по памяти и времени, особенно если они не оптимизированы (например, за счет мемоизации)․
• Сложность отладки: Рекурсивный код может быть сложнее отлаживать и тестировать, чем итеративный․

Оптимизация рекурсивных функций

Когда мы работаем с рекурсией, важно учитывать методы оптимизации, которые могут помочь улучшить производительность․ Одним из популярных методов является мемоизация, которая позволяет сохранять результаты предыдущих вычислений:

const memo = {};
function fibonacci(n) {
 if (n in memo) return memo[n]; // проверка кэша
 if (n <= 1) return n; // базовый случай
 memo[n] = fibonacci(n ‒ 1) + fibonacci(n ⎯ 2); // сохранение результата
 return memo[n];
}

С помощью мемоизации мы можем значительно улучшить производительность функции Фибоначчи, избегая повторных вычислений․

Рекурсия предлагает более естественный и короткий способ решения многих задач, особенно там, где структуры данных имеют иерархическую природу, такие как деревья и графы․ Несмотря на свои недостатки, рекурсия позволяет создавать более читаемые и поддерживаемые программы․

Подробнее

Рекурсивные алгоритмы	Как работает рекурсия	Примеры рекурсии	Плюсы и минусы рекурсии	Оптимизация рекурсивного кода
Факториал с рекурсией	Деревья и рекурсия	Мемоизация	Обход графов	Сравнение с итерацией