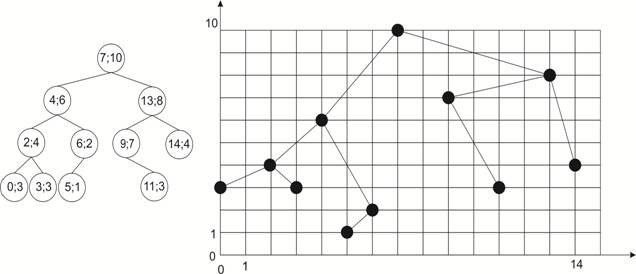
Сортировка деревом (AVL): как обеспечить быструю и эффективную работу с данными

Когда мы говорим о хранении и обработке больших объемов информации, одним из важнейших аспектов является обеспечивание быстрого доступа к данным и их эффективное обновление. Для этого используют разные структуры данных, в т.ч. деревья. Одним из наиболее известных и применяемых видов балансированных деревьев является AVL-дерево.

На протяжении многих лет разработчики сталкиваются с необходимостью искать, вставлять и удалять элементы в структуре данных, которая должна оставаться сбалансированной. Именно для этого создавались деревья типа AVL — они обеспечивают автоматическую балансировку, что значительно повышает производительность операций.

Что такое AVL-дерево и как оно работает?

AVL-дерево — это самобалансирующееся бинарное дерево поиска (БДП), в котором для каждого узла гарантируется балансировка по высоте. Это означает, что разница высот левого и правого поддеревьев любого узла не превышает единицу. Благодаря этому условию высота дерева остается логарифмической относительно количества элементов, что обеспечивает высокую эффективность поиска, вставки и удаления элементов.

Основные характеристики AVL-дерева

• Быстрая сортировка и поиск: благодаря уменьшению высоты дерева, операции поиска выполняются за O(log n).
• Автоматическая балансировка: при вставке и удалении элементов дерево само перестраивается для поддержания балансировки.
• Использование балансирующих вращений: для восстановления равновесия при необходимости.
• Обеспечение эффективности: подходит для систем, где требуется частый доступ к данным в реальном времени.

Как реализовать и поддерживать балансировку AVL-дерева?

Реализация AVL-дерева включает в себя не только создание узлов и вставку элементов, но и сложные операции по восстановлению баланса. После каждой вставки или удаления необходимо определить, не нарушена ли балансировка, и при необходимости выполнить вращения.

Типы вращений и их роль

Тип вращения	Описание	Когда используется
Левое вращение (Left Rotation)	Перестановка узлов, при которой_Right_ поддерево становится корнем, а исходный узел — левым потомком этого.	При right-heavy ситуации (правом перевесе).
Правое вращение (Right Rotation)	Перестановка узлов, при которой_левое_ поддерево становится корнем, а исходный узел — правым потомком этого.	При left-heavy ситуации (левом перевесе).
Левое-правое вращение (Left-Right Rotation)	Комбинация двух вращений, используется при сложных случаях балансировки.	При ситуации, когда левый потомок имеет правого перевеса.
Правое-левое вращение (Right-Left Rotation)	Комбинация двух вращений, применяется при противоположной ситуации.	Когда правый потомок имеет левого перевеса.

Практическое применение AVL-деревьев

Данная структура данных нашла широкое применение в различных областях. Ниже представлен список наиболее популярных сфер:

1. Базы данных: индексы в реляционных базах данных используют балансированные деревья для быстрого поиска и обновления данных.
2. Файловые системы: организации хранения файлов, где важна быстрая навигация и изменение структуры данных.
3. Информационные системы и поисковые движки: обеспечение быстрого доступа к информации.
4. Обработка больших данных: при необходимости динамического обновления данных без снижения производительности.

Преимущества и недостатки AVL-деревьев

Преимущества

• Высокая скорость: операции поиска, вставки и удаления выполняются за логарифмическое время.
• Автоматическая балансировка: исключает необходимость ручной корректировки структуры.
• Универсальность: подходят для систем с высокими требованиями к скорости обработки данных.

Недостатки

• Сложность реализации: требуются знания алгоритмов вращений и балансировки.
• Обработка большого количества вращений: может немного снизить скорость при частых операциях вставки и удаления, особенно в невысоких объемах данных.
• Память: потребление дополнительных ресурсов для хранения информации о высоте узлов и балансирующих факторах.

Пример реализации AVL-дерева на практике

Для более глубокого понимания, давайте рассмотрим пример типичных этапов вставки элемента в AVL-дерево и восстановления его баланса. Представим, что мы вставляем новый узел, и после этого необходимо определить, нарушена ли балансировка, и какие вращения при этом понадобятся.

Пошаговая вставка и балансировка

1. Вставляем элемент согласно правилам бинарного поиска — слева, если меньше, справа — если больше.
2. Обновляем информацию о высотах узлов для всех родительских узлов.
3. Проверяем баланс узлов, начиная с вставленного, вверх по дереву.
4. Если баланс нарушен (разница высот > 1), выполняем соответствующие вращения.
5. Обновляем высоты после вращений.

Если наша задача — организовать максимально эффективное хранение и быстрый доступ к данным, то AVL-дерево является отличным решением. Оно позволяет соблюдать баланс в структуре данных, что гарантирует высокий уровень производительности при работе с большими объемами информации. Однако для реализации требует определенных знаний и внимательности. В конечном итоге, выбор структуры зависит от конкретных требований проекта и условий эксплуатации.

Поддерживание баланса в деревьях данных, таких как AVL, крайне важно для ускорения поиска, так как высота дерева определяет количество шагов, необходимых для нахождения элемента. Небалансированное дерево может превратиться в список, что снизит эффективность операций до O(n). Сбалансированное дерево, наоборот, гарантирует, что все операции выполняются за логарифмическое время, что значительно повышает производительность системы в целом.

Подробнее

Линейные запросы	Обеспечение скорости поиска	Динамическое обновление данных	Обеспечивание надежности хранения	Эффективность для больших объемов данных
поиск элементов в дереве	оптимизация операций вставки	удаление и изменение данных	поддержка больших баз данных	эффективность при обработке больших данных