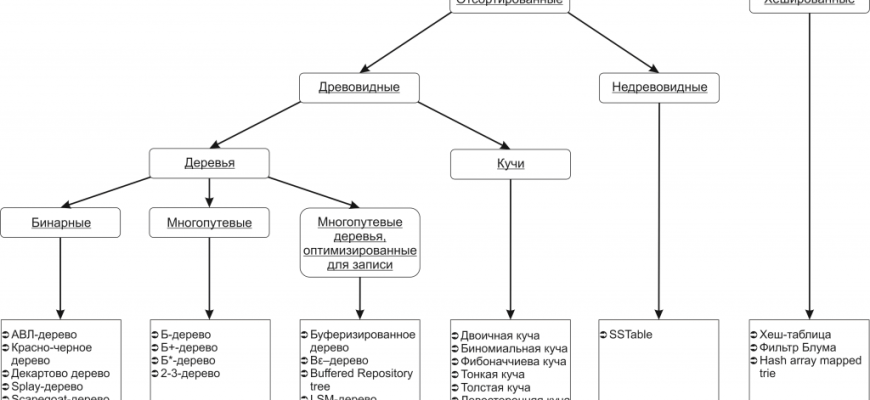
- Сортировка деревом (AVL): как сбалансированные деревья делают поиск быстрее
- Что такое дерево AVL и почему оно важно?
- Основные понятия и архитектура дерева AVL
- Что такое бинарное дерево поиска?
- Что такое балансировка?
- Основные операции в дереве AVL
- Механизм балансировки: ротации и их виды
- Пошаговый пример вставки и балансировки
- Допустим, мы вставляем элементы: 10, 20, 30
- Практическое применение дерева AVL
- Плюсы и минусы дерева AVL
- Какой лучший способ балансировки дерева для быстрых операций поиска: AVL или другие?
Сортировка деревом (AVL): как сбалансированные деревья делают поиск быстрее
В нашей повседневной жизни мы сталкиваемся с множеством задач, связанных с хранением и поиском информации. Представьте себе библиотеку, где книги расставлены в случайном порядке — поиск нужной книги может занять много времени. А что если организовать их так, чтобы постоянно находить книгу за доли секунды? Именно для этого и существуют структуры данных — такие, как деревья, и в частности, самобалансируемое дерево AVL.
В этой статье мы разберём, что такое дерево AVL, как оно работает, почему оно считается одним из эффективных способов организации данных, и какие преимущества оно дает в реальных приложениях. Мы расскажем вам всё, что нужно знать, чтобы понять принцип работы этого удивительного алгоритма и даже применить его в своих проектах.
Что такое дерево AVL и почему оно важно?
Дерево AVL — это вид самобалансирующегося бинарного дерева поиска, названное в честь своих создателей — Георгия Адольфовича Адельсона-Вельского и Евгения Михайловича Ландау, которые предложили его в 1962 году. Название расшифровывается как AVL Tree, где каждая буква — инициалы авторов.
Главная идея дерева AVL — поддерживать баланс между левым и правым поддеревьями каждого узла так, чтобы разница — так называемый height баланса — не превышала единицу. Это обеспечивает сбалансированную структуру, которая предотвращает превращение дерева в список, то есть очень длинную цепочку, в которой поиск превращается в линейную операцию.
Если дерево становится не сбалансированным после вставки или удаления узлов, оно автоматически выполняет серию перестановок — так называемых реверсий (rotation) — для восстановления равновесия. Именно это делает дерево AVL очень эффективным для поиска, вставки и удаления элементов за логарифмическое время, что значительно быстрее по сравнению с неструктурированными массивами или списками.
Основные понятия и архитектура дерева AVL
Что такое бинарное дерево поиска?
Перед тем как разбираться в деталях дерева AVL, важно понять, что такое бинарное дерево поиска (Binary Search Tree, BST). Это структура данных, в которой каждый узел содержит ключ (значение), и для каждого узла значение в левом поддереве меньше, а в правом — больше. Такой порядок обеспечивает быструю навигацию и поиск элемента.
Однако обычное BST может стать очень неуравновешенным — например, при последовательной вставке отсортированных данных оно превращается в цепочку, что затрудняет быстрый поиск. Именно баланс поддерживается в дереве AVL.
Что такое балансировка?
Балансировка — это процесс поддержания разницы высот поддеревьев каждого узла на уровне не более 1. Высота узла — это длина самого длинного пути от этого узла до листа. Если разница высот превышает единицу, дерево считается не сбалансированным, и требуется выполнить перестановку для восстановления баланса.
Балансировка обеспечивает, что высота дерева остается логарифмической относительно количества элементов, что и обеспечивает эффективность операций поиска и редактирования.
Основные операции в дереве AVL
Рассмотрим, какие операции присутствуют в дереве AVL и как они достигают целей быстрого поиска:
- Вставка — добавление нового узла осуществляется по тому же принципу, что и в BST, с последующей проверкой баланса и выполнением ротаций при необходимости.
- Удаление — удаление узла, после которого также проводится проверка баланса и при необходимости — ротации, чтобы сохранить баланс дерева.
- Поиск — быстрый благодаря упорядоченной структуре, позволяет находить элемент за логарифмическое время.
Механизм балансировки: ротации и их виды
Важной частью работы дерева AVL являются ротации, процессы перестановки узлов для восстановления баланса. Их существует три основных вида:
| Тип ротации | Описание | Когда применяется |
|---|---|---|
| Левый поворот (Left Rotation) | Поворот вправо, чтобы сбалансировать дерево при доминировании правого поддерева | Когда левое поддерево слишком высоко по сравнению с правым |
| Правый поворот (Right Rotation) | Поворот влево при избытке высоты левого поддерева | Когда правое поддерево слишком высоко по сравнению с левым |
| Левый-контра-L или правый-контра-R (Left-Right и Right-Left) | Комбинированные ротации для сложных случаев (например, когда поддерево с одной стороны перерастает и вызывает дисбаланс) | Когда возникают сложные ситуации со смешанными несбалансированными ветвями |
Пошаговый пример вставки и балансировки
Допустим, мы вставляем элементы: 10, 20, 30
Рассмотрим последовательность вставки в дерево AVL и её влияние на баланс:
- Вставка 10: дерево пустое, просто создаем корень с ключом 10.
- Вставка 20: 20 больше 10, идет в правое поддерево, высота дерева увеличивается, баланса не нарушена.
- Вставка 30: вставляется справа от 20, высота правого поддерева увеличивается. Теперь разница высот у корня — 2.
Поскольку баланс нарушен, выполняется правый поворот (rotateRight) для восстановления баланса. В итоге, дерево становится сбалансированным, и поиск занимает только логарифмическое время.
Практическое применение дерева AVL
Такая структура находит широкое применение в различных областях:
- Базы данных — быстрый доступ к записям.
- Файловые системы — организация каталогов и файлов.
- Интернет-поиск — индексация и поиск релевантных данных.
- Реализация словарей и таблиц ассоциаций, эффективное хранение и поиск ключ-значение.
Плюсы и минусы дерева AVL
| Плюсы | Минусы |
|---|---|
| Обеспечивает быструю работу поиска, вставки и удаления | Дополнительные вычислительные затраты на поддержание баланса (ротации) |
| Гарантированное логарифмическое время операций | Сложность реализации по сравнению с простыми структурами |
| Отлично подходит для динамических данных, где часто происходит вставка и удаление | Потребность в балансировке после каждой операции, что иногда снижает скорость при редких обновлениях |
Если вы занимаетесь разработкой систем, где важна стабильная и быстрая работа с большими объемами данных, то дерево AVL — это то решение, которое стоит применить. Его способность сохранять баланс и обеспечивать логарифмическое время операций делает его отличным выбором для множества задач. Конечно, оно требует более сложной реализации по сравнению с простыми структурами, однако преимущества, которые оно дает, этого стоят.
В современном мире, где скорость и эффективность, ключевые показатели, использование сбалансированных деревьев, таких как AVL, становится неотъемлемой частью высокопроизводительных систем. А для нас, разработчиков и аналитиков, понимание их принципов поможет создавать более надежные и быстрые приложения.
Какой лучший способ балансировки дерева для быстрых операций поиска: AVL или другие?
Дерево AVL считается одним из наиболее эффективных вариантов для обеспечения быстрой работы с данными за счет строгой балансировки. Однако есть и другие структуры, например, красно-черные деревья, которые менее строгие в балансировке, но более быстро восстанавливают свойства после вставки или удаления, что в некоторых случаях делает их предпочтительнее. В выбор зависит от конкретных задач: нужен ли строгий баланс или более гибкая и быстрая схема реконструкции.
Подробнее
| Лси запросы к статье | Лси запросы к статье | Лси запросы к статье | Лси запросы к статье | Лси запросы к статье |
| Как работают ротации в дереве AVL | Преимущества балансировки дерева AVL | Структура данных AVL дерево | Самобалансирующееся дерево поиска | Лучшие алгоритмы балансировки деревьев |
| Разница между AVL и красно-черным деревом | Примеры использования дерева AVL | Балансировка при вставке в AVL | Балансировка при удалении в AVL | Оптимизация поиска с помощью дерева AVL |
| Детальные алгоритмы ротации | Эффективность дерева AVL | Области применения сбалансированных деревьев | Структуры данных для быстрого поиска | Обзор алгоритмов балансировки |