Сортировка деревом (AVL): как сохранить баланс и обеспечить скорость работы

В мире современных компьютерных технологий задача организации данных и их быстрого поиска занимает одну из ключевых позиций․ Среди множества алгоритмов и структур данных особое место занимает дерево поиска с автоматической балансировкой — AVL-дерево․ В этой статье мы разберём, что такое AVL-деревья, как они работают, и почему их использование значительно повышает эффективность обработки данных․

Что такое AVL-дерево и его история

AVL-дерево, это разновидность двоичных деревьев поиска, в которых обеспечивается строгий баланс высоты для повышения скорости поиска, вставки и удаления элементов․ Название происходит от фамилий создателей — Георгия Адальберта и Егора Владыкина — которые впервые предложили эту модель в 1962 году․ Именно благодаря их разработке был введён критерий балансировки, который позволяет гарантировать, что высота дерева будет минимальной, а значит, операции на данных займут минимальное время․

Рассмотрим основные особенностиAVL-дерева:

• Каждая вершина содержит ключ или значение, а также указатели на левое и правое поддерево;
• Для каждого узла сохраняется баланс-фактор, разница высоты левого и правого поддеревьев, который всегда лежит в диапазоне от -1 до 1;
• При вставке и удалении элементов происходит автоматическая балансировка дерева за счёт специальных операций (поворотов);

Принципы работы AVL-деревьев

Основной задачей AVL-дерева является поддержание своего баланса при операциях вставки и удаления элементов․ Это достигается за счёт произвольного выполнения вращений — небольших изменений структуры дерева, которые позволяют восстановить баланс после неудачной вставки или удаления․

Баланс-фактор

Для каждого узла вычисляется баланс-фактор — разница высоты левого и правого поддеревьев․ Он принимает значения:

• 0: высота левого и правого поддеревьев одинаковая;
• 1: левое поддерево выше на один уровень;
• -1: правое поддерево выше на один уровень․

Если баланс-фактор выходит за границы диапазона от -1 до 1, то дерево нуждается в балансировке․

Виды вращений

Для восстановления баланса используют четыре типа вращений:

1. Левое вращение: применяется при слишком правом подкреплении дерева;
2. Правое вращение: применяется при слишком левом подкреплении;
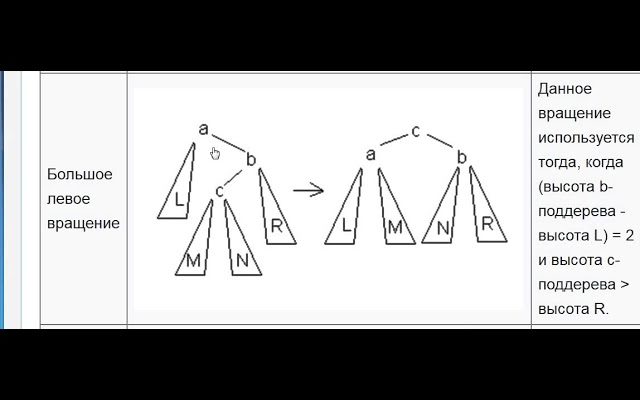
3. Лево-правое вращение: комбинация левого вращения с последующим правым;
4. Право-левое вращение: комбинация правого вращения с последующим левым․

Тип вращения	Когда применяется	Описание
Левое вращение	Когда правое поддерево слишком высоко	Вращение вокруг узла, чтобы снизить высоту правого поддерева
Правое вращение	Когда левое поддерево слишком высоко	Вращение вокруг узла, чтобы снизить высоту левого поддерева
Лево-правое вращение	Когда левое поддерево имеет правого ребенка с высоким балансом	Комбинация правого вращения левого ребенка и последующего левого вращения узла
Право-левое вращение	Когда правое поддерево имеет левого ребенка с высоким балансом	Комбинация левого вращения правого ребенка и последующего правого вращения узла

Алгоритм вставки элемента в AVL-дерево

Процесс вставки элемента в балансированное дерево похож на вставку в обычное двоичное дерево поиска, но с обязательной проверкой и восстановлением баланса после каждой вставки․

Пошаговое описание

1. Проходим по дереву, сравнивая вставляемое значение с текущим узлом, и спускаясь по левым или правым ветвям;
2. Находит подходящее место для вставки и добавляем новый узел;
3. Обратно возвращаемся по пути и проверяем баланс-факторы всех узлов до корня;
4. Если обнаружен узел с баланс-фактором, выходящим за диапазон [-1,1], выполняем соответствующий вид вращения;
5. Повторяем процедуру до корня дерева, чтобы удостовериться в его балансировке․

Пример вставки

Допустим, мы вставляем число 30 в уже существующее AVL-дерево․ После стандартной вставки формируется дисбаланс в одном из узлов․ Для его устранения выполняется соответствующее вращение, и высота дерева возвращается к оптимальному уровню․ В итоге, поиск, вставка и удаление продолжают работать с высокой скоростью благодаря поддержанию баланса;

Удаление элемента из AVL-дерева

Удаление элемента, сложный процесс, требующий особого внимания к сохранению баланса․ После удаления узла в дереве могут появиться дисбалансы, которые устраняются за счёт вращений, аналогичных тем, что применяются при вставке․

Основные этапы удаления

1. Поиск узла для удаления по ключу;
2. Если узел — лист, его просто удаляем;
3. Если у узла есть один дочерний элемент, заменяем его этим элементом;
4. Если у узла два дочерних, ищем его кубинацию (наименьший узел в правом поддереве), его переносим на место удаляемого и удаляем его из поддерева;
5. Обновляем высоты и баланс-факторы на пути «от удаленного узла к корню»;
6. При обнаружении нарушения балансировки выполняем вращения для восстановления баланса․

Преимущества и недостатки AVL-деревьев

Преимущества

• Обеспечивают гарантированно быстрый поиск — операция занимает O(log n) времени;
• Поддержание баланса существенно ускоряет операции вставки и удаления;
• Являются самобалансирующимися, что исключает необходимость сторонних алгоритмов балансировки;
• Используются в системах баз данных, файловых системах, при реализации словарей и других структурах данных․

Недостатки

• Более сложная реализация по сравнению с обычными двоичными деревьями поиска;
• Дополнительные операции вращений могут потреблять ресурсы, особенно при частых обновлениях;
• Для алгоритмов с очень большим количеством вставок и удалений возможно требуется частая балансировка, что увеличивает вычислительные затраты․

Практическое применение AVL-деревьев

На практике AVL-деревья находят широкое применение в тех системах, где важна высокая скорость обработки данных․ Например, в базе данных, где необходимо быстро находить, вставлять или удалять записи, в реализации словарей и ассоциативных массивов, а также в системах, где важна строгая балансировка и минимальные временные затраты на операции․

Кроме того, их используют для реализации различных структур данных, таких как:

• Многопользовательские системы: ускоряют работу с большими объёмами данных;
• Геоинформационные системы: для быстрого поиска географических объектов;
• Искусственный интеллект и игры: для хранения и поиска преимуществ и вариантов решений․

Подытоживая, можно сказать, что AVL-деревья являются мощным инструментом для обеспечения высокой эффективности в структурах данных․ Они позволяют добиться минимальной высоты дерева и предсказуемой скорости выполнения операций, что особенно важно в больших и динамичных системах․ Однако, при разработке собственных решений важно учитывать сложность реализации и требования к ресурсам․

Если вы желаете углубиться в тему и использовать AVL-деревья в своих проектах, рекомендуем тщательно ознакомится с алгоритмами вращений и балансировки, а также провести тестирование на предмет производительности․ В дальнейшем это поможет вам создавать более быстрые и надёжные системы․

Подробнее

Оптимизация поиска в AVL	Реализация вращений в AVL	Балансировка дерева поиска	Пример кода AVL-дерева	Сравнение с red-black tree
AVL-дерево и его свойства	Алгоритм вставки	Обновление баланс-фактора	Преимущества AVL	Недостатки AVL-деревьев
Динамическая балансировка	Балансировка при удалении	Применение в базах данных	Графики эффективности	История развития
Сложность алгоритмов AVL	Практические кейсы	Лучшие практики внедрения	Реализация на C++ и Java	Оптимизация операций
Обновление структуры данных	Балансировка в реальном времени	Использование в системах хранения данных	Плюсы и минусы	Современные аналоги