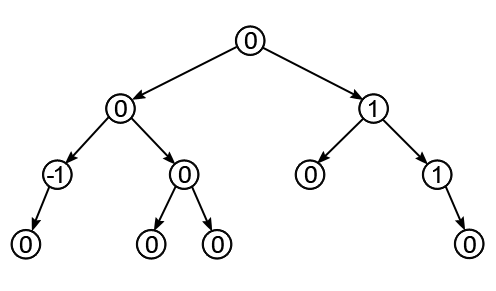
Сортировка деревом (AVL): Максимальная эффективность поиска и балансировки данных

---

Когда мы начинаем говорить о хранении и обработке больших объемов информации, встает вопрос поиска наиболее эффективных методов организации данных․ Одним из таких методов является структура данных, известная как самобалансирующееся бинарное дерево поиска — AVL-дерево․ В этой статье мы разберемся, как оно работает, в чем его преимущества и недостатки, и почему оно считается одним из наиболее популярных решений для быстрого поиска, вставки и удаления элементов․

Что такое AVL-дерево и почему оно важно?

Для начала важно понять, что такое бинарное дерево поиска и чем оно отличается от обычных структур․ Бинарное дерево поиска — это структура данных, где каждый узел содержит значение, а также ссылки на левое и правое поддерево, в которых, соответственно, лежат значения, меньшие или большие, чем значение в текущем узле․ Такой подход обеспечивает быстрый поиск, вставку и удаление элементов․

Однако стандартное бинарное дерево поиска при неправильной организации может стать очень «высоким» и неэффективным — тогда операции ищут долго, приближаясь к линейной․ Поэтому появилась идея поддерживать дерево в сбалансированном состоянии, что и реализуется с помощью специальных правил․ Именно это и делает AVL-дерево — самобалансирующейся структурой данных․

Основные свойства AVL-дерева

Итак, основные характеристики AVL-дерева:

• Бинарное дерево поиска: каждое левое поддерево содержит значения менее текущего узла, а правое — более․
• Баланс-фактор: разница в высоте левого и правого поддеревьев для каждого узла не превышает 1․
• Самобалансировка: при вставке и удалении элементов выполняются операции, обеспечивающие сохранение балансировки․

Как работают операции с AVL-деревом?

Рассмотрим наиболее важные операции: вставку, удаление и балансировку․ Каждая из них обеспечивается с помощью специальных алгоритмических шагов, включающих вращения и пересчёт высот․

Вставка элемента

Процесс вставки в AVL-дерево состоит из двух этапов:

1. Об обычном добавлении: сначала происходит стандартная вставка по правилам бинарного дерева поиска․
2. Балансировка: после вставки проверяются баланс-факторы узлов на пути назад к корню․ В случае нарушения баланса выполняются вращения для восстановления свойств дерева․

Типы вращений при балансировке

• Левое вращение: используется при ситуации, когда левый поддерево становится слишком высоким․
• Правое вращение: аналогично, когда правое поддерево переходит в доминирующее положение․
• Двойное вращение: комбинация левого и правого вращений, применяется при более сложных случаях нарушения баланса․

Удаление элемента

Удаление — более сложный процесс, чем вставка, так как после удаления необходимо также выполнить балансировку всего дерева․ Алгоритм включает:

1. Поиск элемента, который нужно удалить․
2. Удаление элемента в зависимости от ситуации: с нулевым, одним или двумя потомками․
3. Обратное обновление баланс-факторов и выполнение вращений для восстановления баланса․

Примеры операций вставки и удаления

Шаг	Описание	Результат
1	Вставка элемента 30 в дерево	Элемент добавляется как лист, проверка и балансировка
2	Удаление элемента 25 из дерева	Элемент удаляется, возможно — подменяется соседом, и дерево балансируется
3	Выполнение вращений при нарушении баланса	Дерево возвращается в сбалансированное состояние

Преимущества и недостатки AVL-деревьев

Рассмотрим, почему именно AVL-дерево считается одним из лучших вариантов для хранения структурированных данных, и в чем его слабые стороны․

Преимущества

• Высокая скорость поиска — благодаря логарифмической высоте дерева․
• Быстрая вставка и удаление при правильной реализации алгоритмов балансировки․
• Обеспечение строгой балансировки, что предотвращает деградацию дерева в список при неправильной вставке․

Недостатки

• Более сложная реализация по сравнению с обычным бинарным деревом поиска․
• Дополнительные вычислительные затраты на балансировку, особенно при частых операциях вставки/удаления․
• Может занимать больше памяти из-за хранения балансовых факторов․

Практическое применение AVL-деревьев

Современные системы и программные решения используют AVL-деревья в самых различных областях:

• Базы данных — для индексации и быстрого поиска информации․
• Файловые системы — для организации каталогов и поиска файлов․
• Финансовые системы — для хранения и обработки больших массивов данных в реальном времени․
• Игровая индустрия, для быстрого поиска объектов и управления состояниями игры․

Feedback и опыт показывают, что при правильной реализации AVL-деревья значительно упрощают разработку и повышают производительность систем․

Если мы рассматриваем проводку быстрого поиска и динамическое изменение данных, то AVL-дерево — это действительно мощный инструмент․ Важно помнить, что его эффективность достигается именно благодаря автоматической балансировке, которая обеспечивает быстрый доступ без деградации структуры․ Однако, для максимально эффективного использования необходимо правильно реализовать алгоритмы вращений и балансировки, а также учитывать возможные затраты ресурсов․

Подробнее

AVL деревья + быстрый поиск	балансировка бинарных деревьев + алгоритмы вращений	самобалансирующиеся структуры данных	сложность реализации	применение в базах данных
Лучшая структура для поиска	Балансировка дерева	Алгоритмы вращений	Обновление высот	Поиск по индексам
Оптимизация вставки	Удаление элементов	Высота дерева	Баланс-фактор	Структура данных
Самобалансирующаяся структура	Балансировка	Эффективность поиска	Алгоритмы	Оптимизация
Хранение данных	Поиск и удаление	Быстродействие	Структура дерева	Интерфейсы