Сортировка на основе бинарного дерева поиска: практическое руководство

---

В нашем сегодняшнем обсуждении мы погрузимся в мир алгоритмов сортировки, сосредоточившись на одной из наиболее эффективных и интересных техник — сортировке на основе бинарного дерева поиска․ Этот метод стал настоящим открытием для многих программистов и разработчиков, поскольку он сочетает в себе простоту и эффективность, позволяя сортировать данные быстро и без лишних затрат памяти․

Как многие из нас знают, существует множество алгоритмов сортировки, каждый из которых имеет свои преимущества и недостатки․ Мы не только рассмотрим, как работает сортировка на основе бинарного дерева поиска, но и обсудим, в каких ситуациях её стоит применять․ Приготовьтесь к увлекательному путешествию вглубь алгоритмов и структур данных!

---

Что такое бинарное дерево поиска?

---

Для начала давайте определим, что мы понимаем под бинарным деревом поиска․ Это структура данных, в которой каждый узел содержит значение и ссылки на левое и правое поддеревья․ Структура называется бинарной, потому что каждый узел может иметь не более двух дочерних узлов․

Главное свойство бинарного дерева поиска, это то, что для любого узла все значения в левом поддереве меньше, чем значение самого узла, а все значения в правом поддереве — больше․ Это свойство позволяет быстро осуществлять операции поиска, вставки и удаления, что делает бинарное дерево поиска одним из наиболее эффективных способов организации данных․

---

Преимущества бинарного дерева поиска

---

• Эффективность поиска: Сложность поиска в среднем составляет O(log n), что гораздо быстрее, чем O(n) у несортированных массивов․
• Динамическое изменение: В отличие от массивов, бинарные деревья позволяют легко вставлять и удалять элементы без необходимости их перемещения․
• Простота реализации: Хотя может показаться, что бинарные деревья сложны в реализации, они на самом деле достаточно просты, что делает их доступными для изучения․

---

Как работает сортировка на основе бинарного дерева поиска?

---

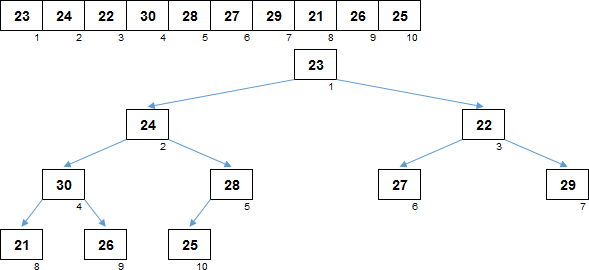
Сортировка на основе бинарного дерева поиска реализуется через два основных этапа: вставка элементов в дерево и последующий обход дерева с целью извлечения отсортированных данных․ Давайте рассмотрим каждый из этих этапов подробнее․

Вставка элементов в бинарное дерево

---

Первым делом мы должны вставить все элементы, которые необходимо отсортировать, в бинарное дерево․ Этот процесс будет осуществляться по следующему принципу:

1. Если дерево пустое, создаётся новый узел корня с записываемым значением․
2. Если значение меньше, чем значение узла, двигаемся влево; если больше, вправо․
3. Повторяем процесс до тех пор, пока не найдём подходящее место для нового узла․

Таким образом, при вставке каждого элемента мы формируем дерево, в котором значения располагаются в соответствии с правилами бинарного дерева поиска․ Это становится основой для последующего обхода и извлечения отсортированных данных․

Обход бинарного дерева для извлечения отсортированных данных

---

На втором этапе мы используем обход дерева, называемый «симметричный обход»․ Он выполняется следующим образом:

1. Переходите в левое поддерево․
2. Посещаете узел (выводите его значение)․
3. Переходите в правое поддерево․

Такой порядок обработки гарантирует, что мы получим элементы в отсортированном порядке․ Это связано с тем, что мы сначала обрабатываем все меньшие значения, затем само значение узла, и, наконец, все большие значения․

---

Пример реализации сортировки на основе бинарного дерева поиска

---

Теперь, когда мы разобрались с теорией, давайте посмотрим на практический пример реализации сортировки на основе бинарного дерева поиска․

class Node:
def __init__(self, key):
self․left = None
self․right = None
self․value = key

def insert(root, key):
if root is None:
return Node(key)
else:
if root․value < key:
root․right = insert(root․right, key)
else:
root․left = insert(root․left, key)
return root

def inorder_traversal(root):
return inorder_traversal(root․left) + [root․value] + inorder_traversal(root․right) if root else []

def sort(arr):
root = None
for key in arr:
root = insert(root, key)
return inorder_traversal(root)

arr = [5, 3, 8, 1, 4, 7, 10]
sorted_arr = sort(arr)
print(sorted_arr)

При выполнении данного кода мы создадим бинарное дерево и отсортируем переданный массив․ На выходе мы получим упорядоченный массив, который может выглядеть так:

Исходный массив	Отсортированный массив
[5, 3, 8, 1, 4, 7, 10]	[1, 3, 4, 5, 7, 8, 10]

---

Когда использовать сортировку на основе бинарного дерева поиска?

---

Сортировка на основе бинарного дерева поиска не всегда является оптимальным выбором․ Вот несколько ситуаций, когда её использование становится особенно актуальным:

• Когда обрабатывается большой объем динамически изменяющихся данных․
• Если нужно часто производить вставку и удаление элементов․
• Когда необходима сортировка, совместимая с другими операциями поиска․

Важно помнить, что наилучших результатов можно добиться, если глубина дерева остаётся логарифмической․ При неблагоприятном распределении данных (например, при вставке элементов в отсортированном порядке), дерево может вырождаться в линейную структуру, что резко снизит производительность․ В таких случаях следует рассмотреть возможность балансировки дерева или использования других структур данных, таких как красно-чёрные деревья или AVL-деревья․

---

Наиболее распространенные ошибки при реализации бинарного дерева поиска включают:

• Необработка случаев, когда дерево пустое․
• Неправильная логика вставки, что может привести к дублированию узлов․
• Ошибки при выполнении обхода дерева, что может привести к некорректной сортировке․

---

Подробнее

бинарное дерево	поиск	алгоритм	данные	сортировка
программирование	структуры данных	оптимизация	производительность	древовидные структуры