Сортировка с минимальным количеством обменов (свопов): секреты эффективных алгоритмов

Когда речь заходит о сортировке‚ большинство из нас вспоминает стандартные алгоритмы — пузырьковую сортировку‚ сортировку вставками или быструю сортировку. Но что делать‚ если нам нужно отсортировать массив или список максимально быстро и при этом минимизировать количество обменов элементов?

В этой статье мы расскажем о том‚ как можно добиться минимальных свопов при сортировке‚ в чем заключается суть таких алгоритмов‚ и какие подходы позволяют оптимизировать операцию обмена элементов. Мы подготовили практическое руководство‚ которое поможет вам понять‚ как использовать алгоритмы сортировки с минимальными обменами в различных прикладных задачах — от обработки больших данных до структур данных‚ где важна экономия ресурсов.

---

Что такое сортировка с минимальными обменами?

В основе сортировки с минимальными обменами лежит идея максимальной уменьшения количества свопов, операций обмена двух элементов массива для их правильного расположения. В отличие от классических алгоритмов‚ в которых обмены могут происходить часто‚ такие подходы стремятся сделать меньше движений‚ чтобы повысить эффективность.

Такая стратегия особенно важна‚ когда операции обмена дорогостоящие или влечут за собой дополнительные издержки — например‚ при обработке больших объемов данных или при работе с элементами‚ перемещение которых дорого в плане времени или ресурсов.

Основные подходы к минимизации обменов

Существует несколько методов и алгоритмов‚ позволяющих добиться минимального количества свопов при сортировке. Рассмотрим наиболее известные из них:

• Топологическая сортировка с минимальным числом операций. Этот подход основываеться на анализе структур данных и ориентации порядка элементов.
• Дерево перестановок и циклы. Алгоритм строит цикл в перестановке и перестраивает его за минимальное число обменов.
• Жадные алгоритмы. Они выбирают наиболее выгодный обмен в каждый момент времени‚ чтобы минимизировать суммарное число свопов.
• Алгоритмы на основе графов. Операции обмена рассматриваются как рёбра в графе‚ а задача, минимизировать их количество.

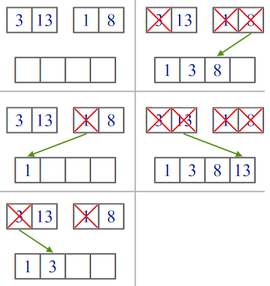
Наиболее эффективный подход — циклы перестановки

Для минимизации свопов важно понять роль циклов в перестановке элементов. Представим‚ что у нас есть массив‚ и мы рассмотрим его перестановку — как элементы меняются местами относительно отсортированного варианта. Тогда каждый цикл этой перестановки можно исправить за число элементов в цикле минус один обменов.

Именно этот принцип лежит в основе методов минимизации операций обмена. Разбираясь с циклами‚ мы можем сделать эффективную перестановку за такое же число свопов‚ как и теоретически возможно‚ без лишних перемещений.

Этап	Действие	Обоснование
1	Определение циклов перестановки	Находим замкнутые циклы элементов‚ которые нуждаются в перестановке
2	Обработка каждого цикла	Переставляем элементы цикла за число элементов — 1 обменов
3	Общий результат	Общее число обменов — сумма по всем циклам‚ что минимально возможное значение

Реализация этого подхода достаточно проста и наглядно демонстрирует‚ как легко добиться минимального числа свопов при сортировке.

Практическая реализация алгоритма минимальных свопов

Переходим к конкретике и рассмотрим пример реализации на языке программирования Python‚ который легко адаптировать под любые ваши нужды. Ниже приведена функция‚ реализующая сортировку с минимальным количеством обменов‚ использующая циклы перестановки:

def min_swaps_sort(arr):
 n = len(arr)
 arr_pos = list(enumerate(arr))
 arr_pos.sort(key=lambda it: it[1])
 visited = [False] * n
 swaps = 0
  for i in range(n):
 if visited[i] or arr_pos[i][0] == i:
 continue
 cycle_size = 0
 j = i
 while not visited[j]:
 visited[j] = True
 j = arr_pos[j][0]
 cycle_size += 1
 if cycle_size > 0:
 swaps += (cycle_size ⎻ 1)
 return swaps

Эта функция не только показывает‚ как просчитать минимальное число свопов‚ но и служит основой для дальнейших алгоритмов сортировки‚ минимизирующих обмены.

Практическое применение

Задачи‚ в которых важны именно минимальные обмены‚ встречаются в самых разных сферах:

• Обработка больших данных. Минимизация перемещений помогает ускорить работу систем обработки информации.
• Организация памяти и кэша. Меньшее количество движений – меньше сбоев и задержек.
• Работа с дорогостоящими операциями обмена. Например‚ при переносе элементов‚ связанных с внешней памятью или сетью.
• Оптимизация структур данных. Например‚ при реорганизации ссылок или узлов.

Когда и зачем использовать алгоритмы с минимальными обменами?

Рассмотрим практические сценарии‚ в которых минимизация свопов принципиальна для достижения эффективности:

1. Обработка массивов с тяжелыми элементами. Если перенос элементов — ресурсозатратная операция‚ то каждый обмен должен быть оправдан.
2. Реализация систем‚ чувствительных к задержкам. В реальном времени важно минимизировать операции‚ чтобы снизить время отклика.
3. Оптимизация в задачах‚ связанных с внешней памятью. Например‚ минимизация чтений/запросов усложнена и дорогостоящая.
4. Предотвращение лишних операций при сортировке больших множеств данных. Особенно актуально при работе с базами данных и облачными системами.

Ключевое преимущество таких алгоритмов — их эффективность в специальных условиях‚ где цена операции обмена критична.

---

Важные нюансы и ограничения

Несмотря на привлекательность сортировки с минимальным количеством обменов‚ важно понимать некоторые ограничения этой методики:

• Не всегда самый быстрый по времени алгоритм. Минимизация свопов не гарантирует минимальное время выполнения‚ зачастую алгоритмы‚ минимизирующие обмены‚ требуют дополнительных расчетов.
• Сложность реализации. В некоторых случаях поиск циклов и перестановок усложняет алгоритм по сравнению с классическими методами сортировки.
• Неэффективность на уже отсортированных данных. В таких случаях простые алгоритмы уже имеют минимальные обмены‚ и дополнительная оптимизация необязательна.

---

Подведение итогов и рекомендации

Сегодня мы рассмотрели основные принципы сортировки с минимальным количеством свопов‚ алгоритмы‚ которые позволяют эффективно реализовать такую сортировку‚ а также практические примеры и сценарии использования.

Если вы работаете с задачами‚ где важна минимизация операций обмена‚ стоит обратить особое внимание на циклы перестановки. Такой подход не только экономит ресурсы‚ но и раскрывает новые возможности в оптимизации программных решений.

Помните‚ что выбор метода зависит от конкретных требований задачи — времени выполнения‚ затрат ресурсов и сложности реализации. В большинстве случаев компромисс между скоростью и экономией обменов позволяет добиться оптимальных результатов.

Ответ на главный вопрос

Подробнее

минимальные свопы при сортировке массивов	циклы перестановки в сортировке	алгоритмы минимизации обменов	проходы по графам при сортировке	оптимизация операций обмена
эффективная перестановка элементов	сложность сортировки с минимальными свопами	использование графов в сортировке	прямой пример реализации	преимущества минимальных свопов
процесс минимизации перемещений	инструменты для оценки свопов	сравнение алгоритмов сортировки	примеры использования в бизнесе	ограничения методов минимизации
устойчивость алгоритмов	значение циклов в перестановке	сложность реализации	параллельные подходы	эффективность на крупных данных