Сортировка с помощью дерева балансировки: Погружение в AVL и красно-чёрные деревья

---

В мире программирования мы часто сталкиваемся с задачами, которые требуют высокой эффективности и оптимизации. Сортировка данных — одна из таких задач, и здесь на помощь приходят структуры данных, такие как AVL- и красно-чёрные деревья. Эти деревья способности балансировать себя, обеспечивают быстрое выполнение операций поиска, вставки и удаления, что делает их незаменимыми в современных алгоритмах сортировки. Давайте погрузимся в детали этих мощных инструментов и рассмотрим, как они работают.

Что такое сбалансированные деревья?

---

Сбалансированные деревья представляют собой структуры данных, которые поддерживают определенный порядок элементов для обеспечения быстрого доступа и легкой навигации. Основная идея заключается в том, чтобы гарантировать, что высота дерева остается относительно небольшой относительно количества элементов, тем самым обеспечивая логарифмическое время доступа к данным.

Существует несколько различных типов сбалансированных деревьев, но среди них AVL- и красно-чёрные деревья являются двумя наиболее популярными и эффективными подходами. Они обеспечивают разнообразные режимы поиска и сортировки, что делает их универсальными инструментами для разработчиков и программистов.

Основные преимущества сбалансированных деревьев

---

• Ускорение поиска: Благодаря балансировке деревьев, операции поиска выполняются быстрее.
• Эффективная вставка и удаление: Эта обработка также оптимизирована, что делает работу с данными более эффективной.
• Предсказуемая производительность: Высота дерева контролируется, что обеспечивает предсказуемое время выполнения операций.
• Гибкость: Можно использовать различные стратегии, чтобы справляться с уникальными требованиями приложений.

AVL-деревья: Основы и принципы работы

---

AVL-деревья были первыми сбалансированными деревьями, созданными в 1962 году двумя математиками — Георгием Адельсоном-Вельским и Евгением Ландисом. Названы в честь их создателей, они требуют, чтобы разность высоты левого и правого поддерева для каждого узла не превышала единицы.

Представьте себе, что у нас есть AVL-дерево, состоящее из узлов с различными значениями. После каждой вставки или удаления узла, дерево проверяет, является ли оно сбалансированным — если нет, выполняются необходимые повороты, чтобы восстановить баланс. Это делает операции поиска, вставки и удаления за O(log n).

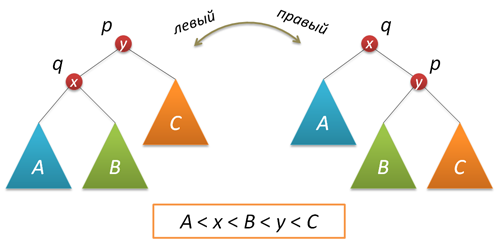
Ротации в AVL-деревьях

---

Для поддержания сбалансированной структуры дерева используются ротации. Существует четыре основных типа ротаций:

1. Левая-Левая (LL) ротация: Используется, когда левое поддерево левого узла заметно больше.
2. Правая-Правая (RR) ротация: Применяется, когда правое поддерево правого узла также больше.
3. Левая-Правая (LR) ротация: Необходима, когда левое поддерево правого узла больше.
4. Правая-Левая (RL) ротация: Используется, когда правое поддерево левого узла больше.

Красно-чёрные деревья: Механика работы

---

Красно-чёрные деревья были предложены в 1972 году и имеют более сложное правило балансировки по сравнению с AVL-деревьями. Основная особенность — каждый узел дерева окрашен в красный или чёрный цвет, и соблюдаются несколько правил, которые гарантируют, что дерево остаётся сбалансированным. Это позволяет минимизировать количество ротаций, необходимых для поддержания баланса при вставке/удалении узлов.

Ключевые правила красно-чёрного дерева:

• Каждый узел является либо красным, либо чёрным.
• Корень всегда чёрный.
• Все листья (NULL-узлы) чёрные.
• Если узел красный, то оба его ребёнка обязательно чёрные.
• Каждый путь от узла до его потомков содержит одинаковое количество чёрных узлов.

Примеры использования красно-чёрных деревьев

---

Красно-чёрные деревья часто используются в системах баз данных и других приложениях, где важны операции, требующие высокой производительности. Эти деревья находят применение в:

• Поддержке ассоциативных массивов.
• Библиотеках, таких как STL в C++.
• Системах управления базами данных для индексирования.

Операция	AVL-дерево	Красно-чёрное дерево
Поиск	O(log n)	O(log n)
Вставка	O(log n)	O(log n)
Удаление	O(log n)	O(log n)
Поддержка баланса	Ротации	Перекраски и ротации

Сравнение AVL и красно-чёрных деревьев

---

Оба этих типа деревьев имеют свои преимущества и недостатки. AVL-деревья обеспечивают строгое балансиование, что делает их более подходящими для операций чтения, которые требуют высокой скорости. В то же время, красно-чёрные деревья облегчают вставку и удаление, так как требуют меньшего числа ротаций.

Таблица сравнения:

Критерий	AVL-дерева	Красно-чёрные деревья
Степень балансировки	Строгое	Умеренное
Сложность операций	Повышенная для вставок	Низкая
Скорость поиска	Быстрее	Медленнее
Применение	Чтение данных	Запись данных

Реализация AVL-деревьев

---

Реализация AVL-деревьев требует детального понимания методов работы с узлами, ротациями и поддержкой баланса. Ниже приведен пример простой реализации AVL-дерева на языке Python:

class Node:
 def __init__(self, key):
 self.left = None
 self.right = None
 self.val = key
 self.height = 1

def insert(root, key):
 # Выполняем стандартную вставку
 if not root:
 return Node(key)
 elif key < root.val:
 root.left = insert(root.left, key)
 else:
 root.right = insert(root.right, key)

 # Обновляем высоту узла
 root.height = 1 + max(getHeight(root.left), getHeight(root.right)))
 # Проверяем баланс
 balance = getBalance(root)

 # Если дерево стало несбалансированным, выполняем ротации
 # Левый левый случай
 if balance > 1 and key < root.left.val:
 return rightRotate(root)

 return root

Для более комплексной реализации потребуется добавить управление ротациями и другие аспекты, но этот код иллюстрирует основные идеи, стоящие за внедрением AVL-деревьев.

Реализация красно-чёрных деревьев

---

Как и с AVL-деревьями, реализация красно-чёрного дерева может быть более сложной, но, тем не менее, здесь представлен базовый шаблон на Python:

class Node:
 def __init__(self, key):
 self.key = key
 self.color = 'red'
 self.left = None
 self.right = None
 self.parent = None

def insert(root, key):
 # Стандартная вставка узла
 new_node = Node(key)
 # ... (вставка кода для размещения узла)
 fix_insert(new_node)

def fix_insert(node):
 # Логика коррекции цвета и ротаций
 while node.parent and node.parent.color == 'red':
 # Реакция на красные узлы
 # ;.. (добавить логику для исправления)

Эта реализация также требует доработки и дополнения, чтобы обрабатывать всевозможные условия и сохранять баланс.

---

Сортировка с использованием деревьев балансировки, таких как AVL и красно-чёрные деревья, является важным аспектом в области программирования. Изучение этих структур и методов обработки данных открывает новые горизонты в оптимизации работы с большими объемами информации.

Надеемся, что это руководство помогло вам лучше понять, как работают сбалансированные деревья, и может послужить основой для ваших будущих проектов. Экспериментируйте с различными реализациями и применяйте полученные знания на практике для достижения новых высот в программировании!

Сбалансированные деревья предлагают ряд преимуществ, в т.ч.:

• Логарифмическое время выполнения операций, что значительно ускоряет задачи сортировки по сравнению с неэффективными методами.
• Поддержка эффективного ведения данных, что позволяет легко вставлять и удалять элементы, не теряя при этом быстродействия.
• Гарантированная сбалансированность, что дает предсказуемые временные затраты на операции.

Подробнее

Особенности AVL-деревьев	Красно-чёрные деревья	Сравнение деревьев	Сравнение по скорости	Коды реализаций
Применения в реальных системах	Плюсы и минусы деревьев	Что такое балансировка?	Понимание структур данных	Оптимизация алгоритмов