Сортировка с помощью деревьев: Погружение в механизм Tree Sort
В мире алгоритмов сортировки существует множество подходов, однако метод сортировки с помощью деревьев, более известный как Tree Sort, занимает особое место благодаря своей эффективности и простоте. Этот алгоритм, построенный на основе двоичных деревьев поиска, не только мило выглядит, но и демонстрирует свойства, которые могут значительно улучшить производительность при работе с большими объемами данных. В данном материале мы собираемся рассмотреть, что такое Tree Sort, как он работает и в каких случаях его стоит применять.
Что такое сортировка с помощью деревьев?
Сортировка с помощью деревьев ౼ это алгоритм, который использует структуру данных «дерево» для организации и сортировки элементов. Алгоритм опирается на свойства двоичного дерева поиска (BST), где для каждого узла дерева выполняется условие: значения всех узлов в левом поддереве меньше значения самого узла, а значения в правом поддереве больше. Таким образом, добавление новых элементов в дерево и последующий их обход в отсортированном порядке позволяет получить последовательность, которая удовлетворяет требованию сортировки.
Деревья являются мощным инструментом, позволяющим производить множество различных операций, в т.ч. вставку, поиск и удаление. Использование деревьев в сортировке обеспечивает логарифмическое время для этих операций в среднем случае, что делает Tree Sort привлекательным выбором для разработчиков и исследователей.
Как работает Tree Sort?
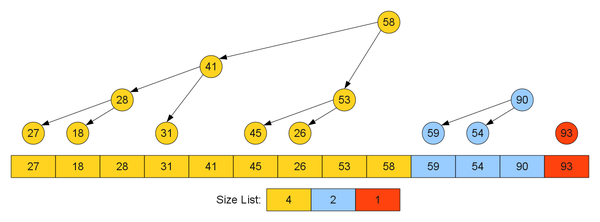
Алгоритм Tree Sort состоит из нескольких ключевых шагов. Прежде всего, мы создаем двоичное дерево поиска и вставляем в него элементы, которые мы хотим отсортировать. Когда все элементы добавлены, мы можем выполнить обход дерева. Наиболее часто используемым приемом обхода для получения отсортированной последовательности является симметричный (инордерный) обход, который обходит левое поддерево, затем корень и, наконец, правое поддерево.
Рассмотрим это более подробно:
- Создание дерева: Для каждого элемента из исходного массива мы создаем узел и вставляем его в дерево. Если значение нового узла меньше текущего узла, мы переходим в левое поддерево, иначе ౼ в правое.
- Сортировка: После завершения вставки всех элементов мы производим симметричный обход дерева, что даст нам элементы в отсортированном порядке.
Преимущества и недостатки
Как и любой алгоритм, Tree Sort имеет свои плюсы и минусы. Рассмотрим их более подробно.
| Преимущества | Недостатки |
|---|---|
|
|
Какова временная сложность алгоритма Tree Sort?
Запомнив структуру двоичного дерева, мы можем выделить несколько сценариев для временной сложности алгоритма Tree Sort. В среднем случае алгоритм работает с временной сложностью O(n log n), что делает его эффективным при сортировке больших массивов данных. Однако в худшем случае, когда дерево становится сильно несбалансированным, временная сложность может вырасти до O(n²), аналогично неэффективным сортировкам. Для предотвращения этого недостатка часто используются сбалансированные деревья, такие как AVL- или красно-черные деревья, которые обеспечивают более стабильную производительность при добавлении и удалении узлов.
Применение Tree Sort
Алгоритм сортировки с помощью деревьев находит применение в различных сферах программирования и обработки данных. Например, он может использоваться в ситуациях, когда:
- Необходимо поддерживать динамическое множество данных, в котором элементы могут добавляться и удаляться;
- Имеется необходимость выполнять частые поиска, вставки и удаления;
- Необходимо отсортировать данные в реальном времени, например, в системах управления потоками данных.
Также стоит отметить, что Tree Sort с лёгкостью комбинируется с другими алгоритмами и структурами данных, что делает его универсальным инструментом для разработчиков. Например, можно интегрировать Tree Sort с хешированием или использовать его в качестве части алгоритмов машинного обучения.
Сортировка с помощью деревьев представляет собой интересный и эффективный способ упорядочивания данных. Кажется, что она является отличным инструментом для программистов, особенно когда дело касается динамических наборов данных. Надеемся, что данная статья поможет вам глубже понять принципы работы этого алгоритма и оценить его сильные и слабые стороны.
Если у вас остались вопросы по алгоритму Tree Sort, будем рады обсудить их в комментариях!
Как Tree Sort сравнивается с другими алгоритмами сортировки?
Сравнивая Tree Sort с другими известными алгоритмами, такими как быстрая сортировка или сортировка слиянием, стоит учитывать множество факторов, в т.ч. структуру данных, типы данных, а также специфику задачи. Быстрая сортировка, как правило, быстрее для статичных массивов, тогда как Tree Sort предлагает значительные преимущества при динамическом добавлении данных. Выбор оптимального алгоритма сортировки зависит от конкретного контекста и требований к производительности, поэтому важно рассматривать каждый алгоритм в отдельности.
Подробнее
| Алгоритмы сортировки | Сравнение алгоритмов | Деревья поиска | Улучшение производительности | Применение алгоритма |
| Сложность алгоритмов | Структуры данных | Интерфейсы программирования | Изучение алгоритмов | Оптимизация кода |