Сортировка с помощью графовых алгоритмов: основы и применение

В современном мире, наполненном информацией и данными, важно находить эффективные способы организации и сортировки информации․ Одним из интересных подходов к этой задаче является использование графовых алгоритмов․ Мы уверены, что понимание концепции сортировки с помощью графов, включая такие алгоритмы, как топологическая сортировка, может значительно улучшить навыки работы с данными и приложениями․ В этой статье мы постараемся развернуто обсудить, что такое графы, как они работают, и каким образом применяются для сортировки данных․

Графы: что это такое?

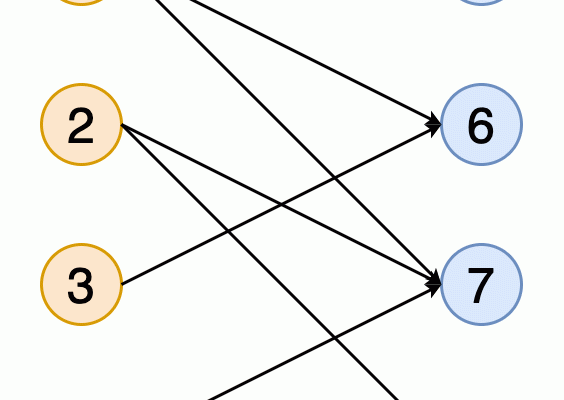
Граф — это математическая структура, состоящая из узлов (вершин) и соединяющих их ребер․ Графы позволяют моделировать различные системы и процессы, начиная от социальных сетей и заканчивая алгоритмами в компьютерных науках․ Важное свойство графов — это способность отражать взаимосвязи между объектами․ Так, используя графы, мы можем визуализировать данные и понимать их структуру․

Существует несколько видов графов, среди которых:

• Ориентированные графы, где грани имеют направление․
• Неориентированные графы, где грани не имеют направления․
• Взвешенные графы, в которых к каждой грани приписан вес․
• Невзвешенные графы, где грани не имеют веса․

Каждый из этих видов графов находит свое применение в различных областях, и понимание их характеристик очень важно для выбора подходящего алгоритма обработки данных․

Топологическая сортировка: что это такое?

Топологическая сортировка — это алгоритм, который работает на ориентированных ациклических графах (ОАГ)․ Главная цель этого алгоритма — отсортировать вершины графа так, чтобы для каждого направленного ребра от вершины A к вершине B вершина A предшествовала вершине B в полученной последовательности․ Топологическая сортировка может быть использована в самых разных ситуациях, например, в планировании задач, где необходимо учитывать зависимости между ними․ Для иллюстрации, представьте организацию выполнения проектов, где одни задачи должны завершаться до начала других․

Существуют два основных алгоритма для реализации топологической сортировки: метод глубинного поиска (DFS) и алгоритм Канфа․ Мы рассмотрим каждый из них подробнее ниже․

Метод глубинного поиска (DFS)

Алгоритм на основеDFS работает следующим образом:

1. Обходим граф в глубину, начиная с произвольной вершины․
2. Помечаем вершины как посещенные․
3. Когда вершина не имеет непосещенных соседей, добавляем ее в начало результата․
4. Повторяем процесс, пока не обойдем все вершины графа;

Такой подход позволяет эффективно обрабатывать граф и получать необходимую последовательность выполнения задач с соблюдением всех зависимостей․

Алгоритм Канфа

Алгоритм Канфа использует другую логику:

1. Сначала вычисляется количество входящих ребер (степень входа) для каждой вершины․
2. Все вершины с нулевой степенью входа добавляются в очередь․
3. Извлекаем вершину из очереди, добавляем ее в результат и уменьшаем степень входа для всех соседей․
4. Если у соседа степень входа стала нулевой, он добавляется в очередь․
5. Процесс повторяется до тех пор, пока не пройдем все вершины․

Алгоритм Канфа также эффективен, предоставляет другой подход к решению и может быть применен в ситуациях, когда нужно учитывать зависимые задачи или проекты․

Применение топологической сортировки в реальной жизни

Топологическая сортировка находит свое применение во множестве областей․ Рассмотрим более подробно несколько примеров ее практического использования:

Область применения	Описание
Планирование задач	Учитывает зависимости между задачами, чтобы определить оптимальную последовательность их выполнения․
Компиляция программного кода	Определяет зависимости между модулями кода для последовательной компиляции․
Производственные процессы	Помогает организовать последовательность действий в производственной цепочке с учетом необходимого порядка операций․

Эти примеры подчеркивают универсальность и эффективность использования топологической сортировки как в математических, так и в практических задачах․

Преимущества и недостатки топологической сортировки

Как и любой алгоритм, топологическая сортировка имеет свои преимущества и недостатки:

Преимущества

• Эффективность в обработке зависимостей․
• Возможность анализа сложных систем с множеством взаимосвязей․
• Универсальность применения в разных областях․

Недостатки

• Необходимость наличия ациклическости в графе для применения алгоритма․
• Сложность реализации для больших графов в зависимости от выбранного метода․

Вопросы и ответы

Основные ограничения при использовании топологической сортировки заключаются в том, что она может быть применена только к ориентированным ациклическим графам (ОАГ)․ Это значит, что если в графе присутствуют циклы, то невозможно определить последовательность, которая удовлетворяла бы всем зависимостям․ Также существуют ограничения по времени обработки для больших графов, что может привести к необходимости использования оптимизированных методов или более простых подходов․

Подробнее

Запрос 1	Запрос 2	Запрос 3	Запрос 4	Запрос 5
Алгоритмы сортировки	Графовые алгоритмы	Ациклические графы	Задачи на графах	Планирование задач
Топологическая сортировка	Методы БД	Поиск в глубину	Динамическое программирование	Обработка данных