Сортировка строк с помощью Counting Sort: Как это работает и почему это важно?
В этой статье мы погрузимся в мир алгоритмов сортировки и разберём механизм работы одного из самых интересных и эффективных методов – сортировки с помощью Counting Sort. Этот алгоритм‚ как и другие‚ имеет свои преимущества и недостатки‚ но он особенно привлекателен при работе со строками. Мы изучим‚ как можно использовать Counting Sort для сортировки строк‚ его практическое применение‚ а также сравним его с другими алгоритмами сортировки;
Counting Sort часто используется в ситуациях‚ когда необходимо сортировать объекты‚ обладающие небольшим диапазоном значений‚ таких как целые числа или‚ в нашем случае‚ символы строк; Этот метод может значительно упростить процесс сортировки‚ благодаря своей линейной временной сложности‚ что делает его одним из самых производительных алгоритмов для некоторых задач.
Что такое алгоритм Counting Sort?
Для начала давайте разберёмся‚ что такое Counting Sort. Этот алгоритм сортировки работает‚ сохраняя количество вхождений каждого значения в отдельном массиве. Затем алгоритм использует эти количество для вычисления позиции каждого элемента в отсортированном массиве. Главное преимущество данного метода заключается в его скорости при работе с небольшими диапазонами целых чисел.
Алгоритм Counting Sort имеет три основных шага:
- Инициализация массива счетчиков.
- Подсчет количества вхождений каждого уникального символа.
Как работает Counting Sort?
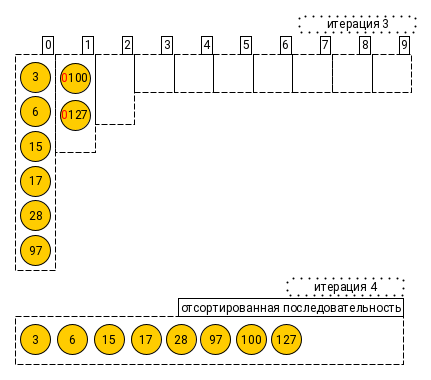
Чтобы лучше понять работу алгоритма‚ рассмотрим процесс шаг за шагом. Предположим‚ у нас есть следующий массив строк:
| Индекс | Строка |
|---|---|
| 0 | banana |
| 1 | apple |
| 2 | cherry |
| 3 | date |
Первый шаг заключается в нахождении максимальной длины строк‚ содержащихся в массиве.
Следующий шаг – инициализация массива для подсчета вхождений символов. После этого мы начинаем проходить по строкам и подсчитывать каждую букву.
На последнем этапе мы составляем новый отсортированный массив на основе результатов подсчета. Этот алгоритм обеспечит нам эффективную сортировку в случае небольшого диапазона символов.
Применение Counting Sort для строк
Теперь‚ когда мы разобрали алгоритм‚ давайте подумаем‚ в каких случаях его можно применять для сортировки строк. Сортировка строк с помощью Counting Sort дает наилучший эффект‚ когда речь идет о строках‚ состоящих из символов определенного диапазона‚ например‚ заглавные и строчные буквы латинского алфавита или цифры.
Применение этого метода может быть актуально в следующих ситуациях:
- Сортировка слов в словарях.
- Сортировка строк‚ полученных из базы данных.
- Обработка текстов для слежения за частотой встречаемости определенных символов.
Сравнение с другими алгоритмами сортировки
Сравнивая Counting Sort с другими алгоритмами сортировки‚ стоит отметить‚ что он наиболее эффективен‚ когда диапазон возможных значений (символов) невелик по сравнению с количеством элементов‚ которые необходимо отсортировать. Например‚ он будет работать существенно быстрее‚ чем стандартные алгоритмы‚ такие как Quick Sort или Merge Sort‚ когда необходимо сортировать строки‚ состоящие из латинских букв и цифр.
| Алгоритм | Лучший случай | Средний случай | Худший случай | Пространственная сложность |
|---|---|---|---|---|
| Counting Sort | O(n + k) | O(n + k) | O(n + k) | O(k) |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) |
Мы рассмотрели теоретическую основу алгоритма Counting Sort‚ его применение к строкам‚ а также сравнили его с другими методами сортировки. Это помогает нам понять‚ что для сортировки строк‚ состоящих из определенного диапазона символов‚ Counting Sort может быть идеальным выбором. Его быстрая и линейная временная сложность позволяет обрабатывать большие объемы данных с высокой эффективностью.
Алгоритм может быть особенно полезным в областях‚ где необходимо быстро обрабатывать текстовые данные‚ включая обработку естественного языка‚ анализ текстовых данных и создание поисковых систем.
Каковы основные преимущества и недостатки алгоритма Counting Sort?
Преимущества: Высокая скорость в определенных условиях‚ простота реализации и возможность обработки больших данных с малым диапазоном значений.
Недостатки: Ограничена приложимость‚ рабочая эффективность снижается при увеличении диапазона значений.
Подробнее
| Сортировка строк | Алгоритмы сортировки | Эффективные алгоритмы | Производительность sorting | Counting Sort применение |
| Сравнение алгоритмов | Сортировка в программировании | Массовая обработка данных | Теория алгоритмов | Оптимизация алгоритмов |