Возрождение рекурсии: как она изменяет алгоритмы сортировки и почему это важно

---

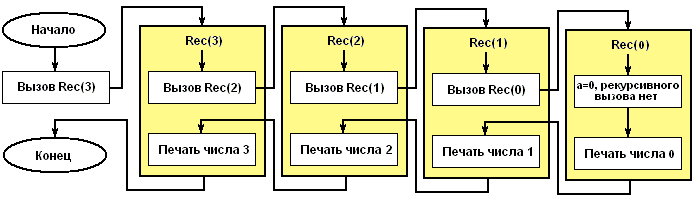
Когда мы рассказываем о классических методах сортировки, часто вспоминаются такие алгоритмы, как пузырьковая сортировка, сортировка вставками или выбором. Однако, среди этого многообразия существует особенный подход, который на первый взгляд кажется загадочным и иногда даже непривлекательным — рекурсия. Только представьте: как можно решать задачу, вызывая саму себя? В этой статье мы подробно рассмотрим, как использование рекурсии кардинально меняет подход к реализации алгоритмов сортировки, делая их более элегантными, понятными и эффективными в определённых ситуациях.

Что такое рекурсия и зачем она нужна в алгоритмах

---

Рекурсия, это метод решения задач, в котором задача разбивается на меньшие по размеру её же части, а решения строится через вызов функции, которая вызывает сама себя. Этот подход особенно полезен при работе с структурами данных (например, деревья или графы) и при реализации алгоритмов сортировки.

Рассмотрим пример: у нас есть массив чисел, который нужно отсортировать. Можно сделать это через классический метод, сравнивая элементы и меняя их местами, однако есть более интуитивно понятный способ — рекурсивный. В основе этого подхода лежит идея деления массива на меньшие подмассивы, сортировки их и объединения результата.

Зачем использовать рекурсию в сортировке?

---

• Элегантность и простота кода: рекурсивные алгоритмы часто выглядят короче и понятнее.
• Модель натурального разбиения: многие задачи логично делятся на похожие подзадачи, что отлично подходит для рекурсии.
• Оптимизация в определённых случаях: при правильной реализации рекурсивные алгоритмы могут работать быстрее или с меньшими затратами ресурсов.

Если говорить о сортировке, то наиболее яркий пример — это быстрое и сортировка слиянием, где рекурсия становится основой их логики.

Классические рекурсивные алгоритмы сортировки

---

Сортировка слиянием (Merge Sort)

Этот алгоритм основан на принципе "разделяй и властвуй". Он разбивает исходный массив на две равные части, рекурсивно сортирует каждую из них, а затем объединяет отсортированные части, образуя итоговый отсортированный массив.

Шаг	Описание
Разбиение	Массив разбивается на две половины (или примерно равные части).
Рекурсивная сортировка	Каждая половина сортируется рекурсивным вызовом.
Объединение	Отсортированные половины сливаются в один отсортированный массив.

Быстрая сортировка (Quick Sort)

Более универсальный и популярный алгоритм, где мы выбираем опорный элемент (пивот), делим массив так, чтобы все элементы меньшие пивота оказались слева, а большие — справа. Затем рекурсивно применяем ту же логику к левым и правым подмассивам.

Шаг	Описание
Выбор пивота	Выбирается центральный или случайный элемент массива.
Разделение	Элементы делятся на две части относительно пивота.
Рекурсивное выполнение	Обрабатываем левую и правую части, вызывая алгоритм для каждого подмассива;

Преимущества и недостатки использования рекурсии для сортировки

---

Рекурсивные алгоритмы сортировки, безусловно, имеют свои плюсы, однако важно помнить и об их недостатках, чтобы сделать правильный выбор в конкретных случаях.

Преимущества

• Простота реализации и читаемость кода.
• Логическая ясность — отражение естественной структуры задачи.
• Эффективность при правильной настройке, особенно на больших данных и при использовании оптимизированных методов (например, сортировка слиянием).

Недостатки

• Риск переполнения стека вызовов при большом количестве рекурсивных вызовов.
• Может требовать дополнительных ресурсов памяти.
• Не всегда обеспечивает лучшую производительность по сравнению с итеративными методами в некоторых случаях.

Практические советы по использованию рекурсии в алгоритмах сортировки

---

Общая рекомендация — применять рекурсию там, где задача логически хорошо делится на подзадачи. Для сортировок это, как правило, разбиения массива. Однако, важно помнить о нескольких практических нюансах.

Несколько советов:

1. Границы рекурсии: всегда устанавливайте условие выхода из рекурсивных вызовов, чтобы не привести к бесконечной рекурсии.
2. Оптимизация: для больших массивов используйте алгоритмы с меньшей глубиной рекурсии или внедряйте итеративные подходы, если есть риск переполнения.
3. Тестирование: проводите тесты на небольших и больших данных, чтобы убедиться в корректности и эффективности.

Практическая реализация рекурсивной сортировки на Python

---

Для закрепления материала приведем пример реализации классической сортировки слиянием (merge sort) на Python с пояснениями и комментариями.

def merge_sort(array):
 if len(array) > 1:
 mid = len(array) // 2
 left_half = array[:mid]
 right_half = array[mid:]

 # рекурсивный вызов сортировки для левой и правой части
 merge_sort(left_half)
 merge_sort(right_half)

 i = j = k = 0

 # слияние отсортированных половин
 while i < len(left_half) and j < len(right_half):
 if left_half[i] < right_half[j]:
 array[k] = left_half[i]
 i += 1
 else:
 array[k] = right_half[j]
 j += 1
 k += 1

 # копируем оставшиеся элементы
 while i < len(left_half):
 array[k] = left_half[i]
 i += 1
 k += 1
 while j < len(right_half):
 array[k] = right_half[j]
 j += 1
 k += 1
 return array

пример использования
arr = [38, 27, 43, 3, 9, 82, 10]
print(merge_sort(arr))

Этот пример показывает, как с помощью рекурсии делим массив, постепенно сортируем его части и объединяем — результат очевиден и очень удобен для понимания.

---

Ответ зависит от конкретных условий и задач. Если вам важна элегантность, читаемость и аккуратное решение для больших данных, рекурсия станет отличным помощником. Однако, важно учитывать возможные риски переполнения стека и выбирать подходящий алгоритм или оптимизацию.

Ответ: Использование рекурсии в алгоритмах сортировки помогает лучше понять такие фундаментальные концепции программирования, как разбиение сложных задач на более простые, управление памятью и вызов функций, а также развитие навыков анализа сложности и эффективности алгоритмов. Рекурсия показывает, как естественно моделировать решения, похожие на человеческое мышление — разбивать проблему на части и решать их поэтапно, что делает обучение программированию более глубоким и осмысленным.

Подробнее

рекурсия в алгоритмах сортировки	лучшие способы использования рекурсии	реализация merge sort	использование рекурсии в алгоритмах	рекурсия и эффективность сортировки
оптимизация рекурсивных алгоритмов	реструктуризация кода с рекурсией	преимущества рекурсивных методов	подводные камни рекурсии в программировании	пример на Python
разница между рекурсией и итерацией	рекурсивное решение задач	структуры данных и рекурсия	рекурсивная сортировка	плюсы и минусы рекурсии