- Все, что нужно знать о сортировке деревом (AVL): как создать сбалансированное дерево и избежать ошибок
- Что такое дерево AVL и зачем оно нужно?
- Основные принципы работы AVL-дерева
- Типы вращений и их назначение
- Как реализовать вставку и удаление в AVL-дереве?
- Алгоритм вставки:
- Алгоритм удаления:
- Особенности реализации и типичные ошибки
- Типичные ошибки при реализации:
- Советы по правильной реализации:
- Практический пример: создание и балансировка AVL-дерева
- Шаги вставки
- Вопрос: Какие основные преимущества использования AVL-дерева по сравнению с обычным бинарным деревом поиска?
Все, что нужно знать о сортировке деревом (AVL): как создать сбалансированное дерево и избежать ошибок
В современном мире, где объем данных растет с невероятной скоростью, эффективность работы с информацией становится как никогда важной. Одним из фундаментальных подходов к организации данных является использование структур данных. Среди них особенно выделяется дерево поиска, которое позволяет быстро находить, добавлять или удалять элементы. Однако, чтобы обеспечить максимальную эффективность, важным аспектом является балансировка дерева. Именно для этого используется алгоритм AVL-дерево, первый в истории самобалансирующийся бинарный поиск. В этой статье мы расскажем о принципах его работы, особенностях реализации и способах избежать типичных ошибок.
Что такое дерево AVL и зачем оно нужно?
Дерево AVL — это разновидность сбалансированного бинарного дерева поиска. В отличие от обычных деревьев, где высоты поддеревьев могут значительно отличаться, в AVL-дереве реализовано строгое ограничение — разница высот левого и правого поддерева каждого узла не превышает одного. Это свойство обеспечивает равномерную структуру, благодаря чему операции поиска, вставки и удаления выполняются за логарифмическое время, что критически важно для больших объемов данных.
Для сравнения, у несбалансированного дерева могут возникать ситуации, похожие на список, когда высота дерева становится равной количеству элементов, что приводит к ухудшению производительности до O(n). В свою очередь, AVL-дерево предотвращает такие ситуации, постоянно гармонизируя структуру. Из-за этого его используют в тех системах, где важна высокая скорость обработки данных, например, в базах данных, поисковых индексах и системах кеширования.
Основные принципы работы AVL-дерева
Ключевое отличие AVL-дерева — это поддержание балансировки на протяжении всех операций. Основные моменты:
- Высоты поддеревьев отличаются не более чем на 1
- После вставки или удаления элементов происходит автоматическая корректировка структуры
- Для балансировки используются балансировка и вращения
Рассмотрим подробнее, какие операции выполняются для поддержания структуры сбалансированной.
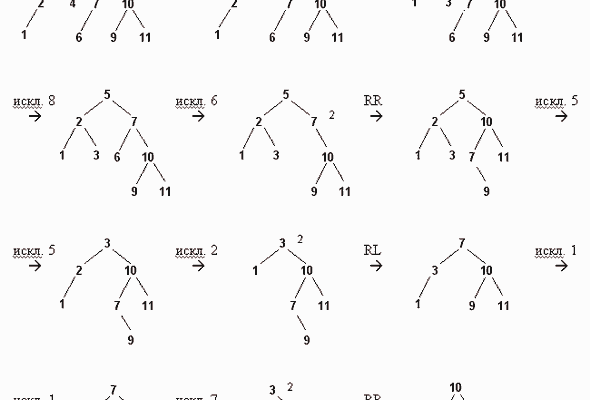
Типы вращений и их назначение
В процессе вставки или удаления узлов в AVL-дереве могут возникать ситуации дисбаланса. Для исправления этих ситуаций используются операции вращения:
- Правое вращение (Right Rotation) — исправляет левый тяжелый дисбаланс
- Левое вращение (Left Rotation) — исправляет правый тяжелый дисбаланс
- Двойное вращение (_Left-Right_ или _Right-Left_) — используется в случаях, когда дисбаланс вызван вложенными ситуациями и требует последовательных вращений
Использование правильных вращений обеспечивает обновление структуры дерева для восстановления сбалансированности без нарушения свойств бинарного поиска.
Как реализовать вставку и удаление в AVL-дереве?
Простая концепция заключается в типичной реализации операций вставки и удаления, аналогичной обычным бинарным деревьям поиска, но с добавлением этапов балансировки. Ниже приведена схема последовательных действий:
Алгоритм вставки:
| Этап | Описание |
|---|---|
| 1. | Вставка нового узла как в обычном бинарном дереве поиска по принципу сравнения значений |
| 2. | Подняться вверх по пути вставки, обновляя высоты узлов |
| 3. | Проверить балансировочный фактор каждого узла (разницу высот левого и правого поддерева) |
| 4. | При обнаружении дисбаланса выполнить соответствующие вращения для восстановления баланса |
Алгоритм удаления:
| Этап | Описание |
|---|---|
| 1. | Найти удаляемый узел (по значению) |
| 2. | Если узел — лист, просто удалить его |
| 3. | Если у узла есть один ребенок, заменить его этим ребенком |
| 4. | Если у узла два ребенка, найти его замену (наименьший узел в правом поддереве), заменить узел, а затем удалить замену из поддерева |
| 5. | Подняться вверх, обновляя высоты и балансировку за счет вращений при необходимости |
Особенности реализации и типичные ошибки
Реализация алгоритмов вставки и удаления в AVL-дереве требует внимания к деталям. Ниже перечислены наиболее распространенные ошибки и способы их избежать.
Типичные ошибки при реализации:
- Неправильное определение баланса: сокращение или неправильное расчет балансировочного фактора приводит к неправильной балансировке дерева
- Забывание обновлять высоты узлов после вращений: это приводит к некорректной работе последующих операций
- Некорректное выполнение двойных вращений: неправильный порядок или неправильные условия могут привести к потере балансировки
- Неправильное удаление узлов с двумя детьми: ошибки в выборе замены и её удалении могут нарушить структуру дерева
Советы по правильной реализации:
- Всегда обновляйте высоты узлов после каждого вращения
- Проверяйте балансировочный фактор сразу после каждой вставки или удаления
- Используйте рекурсивные функции для вставки и удаления, чтобы понять последовательность операций
- Делайте тестирование на случайных данных, включая одновременные операции вставки и удаления
Практический пример: создание и балансировка AVL-дерева
Давайте пройдемся по примеру вставки нескольких элементов и посмотрим, как дерево самостоятельно балансируется. Пусть мы вставляем числа: 30, 20, 40, 10, 25, 35, 50, 5, 15.
После каждой вставки дерево автоматически балансируется с помощью вращений, и итоговая структура остается сбалансированной.
Шаги вставки
- Вставка 30: корень дерева, балансировка не требуется
- Вставка 20: левое поддерево, балансировка не требуется
- Вставка 40: правое поддерево, балансировка не требуется
- Вставка 10: слева от 20, дерево стало чуть более левым, балансировка осуществляется путем правого вращения вокруг 20
- Вставка 25: между 20 и 30, балансировка не требуется
- Вставка 35: между 30 и 40, балансировка не требуется
- Вставка 50: справа от 40, балансировка не требуется
- Вставка 5: слева от 10, вызывается вращение для балансировки
- Вставка 15: между 10 и 20, балансировка
В результате получаем сбалансированное дерево, обладающее высокой скоростью поиска и изменения данных.
Глубокое понимание и правильная реализация алгоритмов вставки, удаления и балансировки делает AVL-дерево незаменимым инструментом для систем, где важна эффективность работы с большими объемами данных. Несмотря на некоторую сложность реализации, его преимущества в скорости и устойчивости оправдывают затраченные усилия. Важнейшее — всегда помнить о необходимости своевременной балансировки и аккуратного обновления высот узлов.
Если вы хотите создать свои системы с динамическим управлением данными, применять AVL-дерево — правильное решение. Поддерживая его структуру, вы значительно повысите скорость и надежность вашего программного продукта.
Вопрос: Какие основные преимущества использования AVL-дерева по сравнению с обычным бинарным деревом поиска?
Основные преимущества AVL-дерева — это гарантированное логарифмическое время выполнения операций поиска, вставки и удаления благодаря автоматической балансировке. Это предотвращает деградацию структуры в виде длинного списка, которая возможна у обычных бинарных деревьев, и обеспечивает высокую производительность при обработке больших объемов данных.
Подробнее
| балансировка деревьев | самобалансирующиеся деревья | вращения в AVL | техника вставки в AVL | алгоритмы удаления в AVL |
| балансировка дерева поиска | самобалансировка структур данных | примеры вращений | реализация вставки в AVL | эффективное удаление данных |
| структуры данных | примеры в программировании | самобалансирующие алгоритмы | стратегии балансировки | улучшение производительности |
| минимизация времени поиска | сбалансированные деревья | процесс балансировки | техники двойных вращений | оптимизация работы с данными |