- Все, что нужно знать о сортировке деревом (AVL): как держать баланс и ускорить поиск
- Что такое AVL-дерево и почему оно важно?
- Вопрос:
- Ответ:
- Основные принципы работы AVL-дерева
- Высота и баланс
- Повороты: основные операции балансировки
- Алгоритм вставки элемента в AVL-дерево
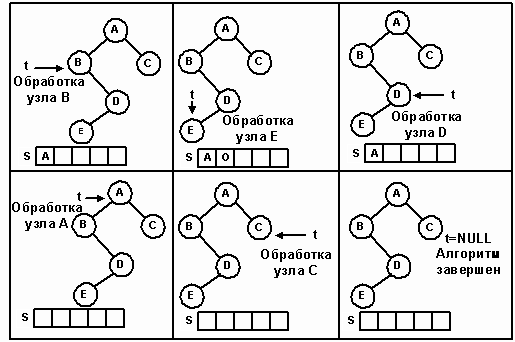
- Пошаговая схема вставки
- Удаление элемента и восстановление баланса
- Преимущества и недостатки AVL-деревьев
- Практическое применение AVL-деревьев
- Вопрос:
- Ответ:
Все, что нужно знать о сортировке деревом (AVL): как держать баланс и ускорить поиск
В современном мире, где данные играют главную роль, эффективность работы с ними становится критически важной задачей. Одним из ключевых структур данных для организации информации являеться дерево поиска, а особым его видом — балансированные деревья, к которым относится AVL-дерево. Мы решили разобраться, что такое сортировка деревом по алгоритму AVL, как она работает, почему именно балансировка играет такую важную роль и как она помогает ускорить операции поиска, вставки и удаления элементов. Если вы хотите понять основы и нюансы работы этого алгоритма, то эта статья, точно для вас.
Что такое AVL-дерево и почему оно важно?
AVL-дерево — это самобалансирующееся бинарное дерево поиска, названное по именам его создателей — Габриэля Адельсона-Вельского и Л. М. Левенштейна. Основная задача такого дерева, постоянно поддерживать баланс, чтобы высота дерева оставалась минимальной, что в свою очередь обеспечивает максимально быструю работу с данными.
При использовании обычных двоичных деревьев поиск, вставка и удаление могут иметь сложность до O(n) в худшем случае, когда дерево превращается в похожее на цепочку. AVL-дерево же делает всё, чтобы этого не произошло, автоматически балансируя свое состояние после каждой операции.
Вопрос:
Как именно AVL-дерево обеспечивает баланс и почему это так важно для производительности?
Ответ:
AVL-дерево использует так называемые "ритуалы балансировки" — после каждой вставки или удаления проверяет высоту своих поддеревьев и, при необходимости, проводит повороты, чтобы восстановить баланс. Такой механизм позволяет сохранять высоту дерева примерно равной log₂(n), что значительно ускоряет операции поиска, вставки и удаления — каждое из них достигает сложности O(log n).
Основные принципы работы AVL-дерева
Рассмотрим ключевые особенности и алгоритмы, которые реализует AVL-дерево, для поддержания своей главной характеристики — балансировки.
Высота и баланс
Для каждого узла дерева высота определяется как максимальная высота его дочерних узлов, плюс один. В AVL-дереве на каждом этапе вставки или удаления проверяются разницы высот левого и правого поддеревьев каждого узла — это называется "балансом".
Если абсолютное значение этого баланса превышает 1, значит, дерево вышло из баланса и требуется его восстановление.
Повороты: основные операции балансировки
| Тип поворота | Описание | Когда применяется |
|---|---|---|
| Левый поворот (Left Rotation) | Используется при чрезмерной тяжелости правого поддерева узла. | Если баланс узла равен -2 и баланс правого ребенка равен -1 или 0. |
| Правый поворот (Right Rotation) | Используется при чрезмерной тяжелости левого поддерева узла. | Если баланс узла равен +2 и баланс левого ребенка равен +1 или 0. |
| Левый-кольцевой (Left-Right) поворот | Комбинация правого и левого поворота, применяется при определенных балансах. | Если баланс узла равен +2, а баланс левого ребенка равен -1. |
| Правый-левый (Right-Left) поворот | Комбинация левого и правого поворота. | Если баланс узла равен -2, а баланс правого ребенка равен +1. |
Благодаря этим операциям дерево восстанавливает свой баланс и продолжает обеспечивать быструю работу с данными.
Алгоритм вставки элемента в AVL-дерево
Процесс вставки нового элемента в AVL-дерево состоит из нескольких шагов:
- Вставка элемента по обычной схеме поиска места в бинарном дереве поиска.
- Обновление высот всех узлов, прошедших путь вставки.
- Проверка баланса каждого узла по пути обратно к корню.
- При обнаружении нарушения балансировки — выполнение одного из вариантов поворотов для восстановления баланса.
Данный алгоритм гарантирует, что после каждой вставки высота дерева не выйдет за логарифмический предел.
Пошаговая схема вставки
| Шаг | Действие | Описание |
|---|---|---|
| 1 | Расположение элемента | Находим место для вставки, согласно правилам бинарного поиска. |
| 2 | Обновление высот | Проходим вверх по дереву, пересчитывая высоты. |
| 3 | Проверка баланса | Определяем, есть ли нарушения. |
| 4 | Балансировка | При необходимости — выполняем повороты. |
Удаление элемента и восстановление баланса
Удаление элемента из AVL-дерева тоже сопровождается проверкой и восстановлением баланса, так как это может нарушить структуру. Процесс похож на обычное удаление в бинарном дереве поиска, но после него, обязательно обновляются высоты и выполняются необходимые повороты.
Этапы удаления:
- Нахождение нужного узла.
- Удаление по классической схеме (удаление листа, узла с одним ребенком или двумя).
- Обновление высот и балансировка вверх по дереву.
Преимущества и недостатки AVL-деревьев
Ключевые преимущества:
- Обеспечивают гарантировано логарифмическую высоту дерева.
- Быстрый поиск, вставка и удаление элементов — O(log n).
- Автоматическая балансировка после каждой операции.
Однако есть и недостатки:
- При частых операциях вставки и удаления могут возникать дополнительные накладные расходы на балансировку—повороты.
- Более сложная реализация по сравнению с обычным двоичным деревом поиска.
Практическое применение AVL-деревьев
AVL-дерева широко используются в задачах, где важна скорость поиска и обновления данных:
- Базы данных и системы хранения информации.
- Файловые системы и кэширование.
- Реализация внутренних структур данных в языках программирования.
- Обработчики событий и системные журналы — где важна скорость сортировки и поиска.
Рассказав обо всех тонкостях алгоритма AVL-дерево, мы понимаем — это мощный инструмент, позволяющий поддерживать структурированные данные в максимально оптимизированном виде. Балансировка и корректные повороты — ключ к тому, чтобы деревья оставались быстрыми и эффективными, даже при очень больших объемах информации. Конечно, реализация алгоритма требует внимательности и аккуратности, ведь любой неправильный поворот или недосмотр могут сломать всю систему. Однако преимущества, которые дает AVL-дерево, — очевидны. Надеемся, наша статья помогла вам понять основы этого замечательного алгоритма и вдохновит на применение его в собственных проектах.
Вопрос:
Что лучше выбрать для хранения данных — обычное бинарное дерево поиска или AVL-дерево?
Ответ:
Если важна скорость операций поиска, вставки и удаления, особенно при работе с большими объемами данных, то лучше использовать AVL-дерево или другие виды сбалансированных деревьев. Обычное бинарное дерево поиска может деградировать до цепочки при неправильной вставке данных, что ухудшает сложность до O(n). Балансированные деревья, такие как AVL, обеспечивают стабильную сложность O(log n) для большинства операций и, следовательно, предпочтительны для критичных к скорости приложений.
Подробнее
| ЛСИ Запрос 1 | ЛСИ Запрос 2 | ЛСИ Запрос 3 | ЛСИ Запрос 4 | ЛСИ Запрос 5 |
|---|---|---|---|---|
| балансировка деревьев поиска | AVL-дерево алгоритм | это такое дерево поиска | повороты в деревьях | есть ли альтернатива AVL |
| преимущества балансированных деревьев | высота AVL-дерева | применение AVL-деревьев | сравнение деревьев поиска | разница между деревьями поиска |
| разработка алгоритма вставки | как сохранить баланс дерева | балансировка при удалении | минимальная высота дерева | структура данных AVL |
| в чем разница AVL и красно-черное дерево | что такое сбалансированное дерево | лучшие структуры данных для поиска | плюсы и минусы AVL | краткий обзор структуры AVL |